“今日头条”杯2018年湖北省赛（网络赛）

这次我们队一共写了5道题，ABCD加F。A和D是简单模拟，B是基础计算几何，C是基础数论，F是图论。别的题都无能为力了，E题卡了很久也没弄出来。不多说了，补题要紧。

A. GSS and CQ（模拟）

• time limit per test：1 second
• memory limit per test：512 megabytes
• input：standard input
• output：standard output

CQCQCQ this is BG6TOE Bravo Golf Six Tango Oscar Echo BG6TOE

In amateur radio communication, every ham has his or her call sign, which is a sequence (the length of which is no more than 6) of letters and digits, for example, GSS's call sign is BG6TOE, where B means HAM from Mainland China, and G means the type of radio station, and 6 means Hubei Province, Anhui Province or Jiangxi Province, then TOE is the suffix, in some cases (e.g. just call someone who is on the channel), call TOE instead BG6TOE is enough.

To start a call, you cal use CQ, the correct way to call is to: Say CQ for three times, e.g. CQCQCQ and then Your call sign, e.g. BG6TOE, for three times, the second time should use NATO Alphabet.

Other parts are optional, for a typical CQ call, one may say:

CQCQCQ this is

Given a list of call signs, your task is to determine what thay would say in the format above.

A : Alfa    | J : Juliett  | S : Sierra  | 1 : One   
B : Bravo   | K : Kilo     | T : Tango   | 2 : Two   
C : Charlie | L : Lima     | U : Uniform | 3 : Three 
D : Delta   | M : Mike     | V : Victor  | 4 : Four  
E : Echo    | N : November | W : Whiskey | 5 : Five  
F : Foxtrot | O : Oscar    | X : Xray    | 6 : Six 
G : Golf    | P : Papa     | Y : Yankee  | 7 : Seven
H : Hotel   | Q : Quebec   | Z : Zulu    | 8 : Eight
I : India   | R : Romeo    | 0 : Zero    | 9 : Nine 

The pure text version of the table above can be found at the link below:

http://acm.whu.edu.cn/upload/2018/whupc/nato.txt

Input

Input contains multiple lines, please process to the end of input.

Each line contains a valid call sign.

Output

For each line of input, output one line with the CQ call in the description above.

Example

BG6TOE
bg6rr
bA1Aa
m0xpd

CQCQCQ this is BG6TOE Bravo Golf Six Tango Oscar Echo BG6TOE
CQCQCQ this is BG6RR Bravo Golf Six Romeo Romeo BG6RR
CQCQCQ this is BA1AA Bravo Alfa One Alfa Alfa BA1AA
CQCQCQ this is M0XPD Mike Zero Xray Papa Delta M0XPD

Note

You should note that both input and output are Case Insensitive

题意

只需要将输入的字符串的每个字母转换为相应的字符串即可。

题解

使用map<char, string>就可完成，注意输入与输出都不区分大小写。

代码

#include <iostream>
#include <algorithm>
#include <cctype>
#include <map>
using namespace std;

map<char, string> s;

void init()
{
    s['A'] = "Alfa";
    s['B'] = "Bravo";
    s['C'] = "Charlie";
    s['D'] = "Delta";
    s['E'] = "Echo";
    s['F'] = "Foxtrot";
    s['G'] = "Golf";
    s['H'] = "Hotel";
    s['I'] = "India";
    s['J'] = "Juliett";
    s['K'] = "Kilo";
    s['L'] = "Lima";
    s['M'] = "Mike";
    s['N'] = "November";
    s['O'] = "Oscar";
    s['P'] = "Papa";
    s['Q'] = "Quebec";
    s['R'] = "Romeo";
    s['S'] = "Sierra";
    s['T'] = "Tango";
    s['U'] = "Uniform";
    s['V'] = "Victor";
    s['W'] = "Whiskey";
    s['X'] = "Xray";
    s['Y'] = "Yankee";
    s['Z'] = "Zulu";
    s['0'] = "Zero";
    s['1'] = "One";
    s['2'] = "Two";
    s['3'] = "Three";
    s['4'] = "Four";
    s['5'] = "Five";
    s['6'] = "Six";
    s['7'] = "Seven";
    s['8'] = "Eight";
    s['9'] = "Nine";
}

int main()
{
    string a;
    while (cin >> a)
    {
        init();
        transform(a.begin(), a.end(), a.begin(), ::toupper);
        cout << "CQCQCQ tHis Is " << a;
        for (int i = 0; i < a.length(); ++i)
            cout << " " << s[a[i]];
        cout << " " << a << endl;
    }
    return 0;
}

B. GSS and Interesting Sculpture（数论）

• time limit per test：1 second
• memory limit per test：512 megabytes
• input：standard input
• output：standard output

GSS is painting an strange sculpture, the sculpture contests of two balls and they may intersect. Your task is to calculate the area of the surface of the sculpture.

Input

Input contains multiple cases, please process to the end of input.

For each line, there are three integers, R, r, L, R and r the radius of the two balls, (L) is the distance of the center of two balls.

0 < R, r, L ≤ 100, |R - r| < L ≤ |R + r|

Output

For each input, output one line with the answer, the area of the surface of the sculpture. Let the standard answer be (a), and your answer be (b), your answer will be considered as correct if and only if $\frac{|a-b|}{max(a, 1)} < 10 ^{-6}$.

Example

3 4 5
3 3 3
1 2 3

271.433605270158
169.646003293849
62.831853071796

题意

求两个可相交球体的表面积。

题解

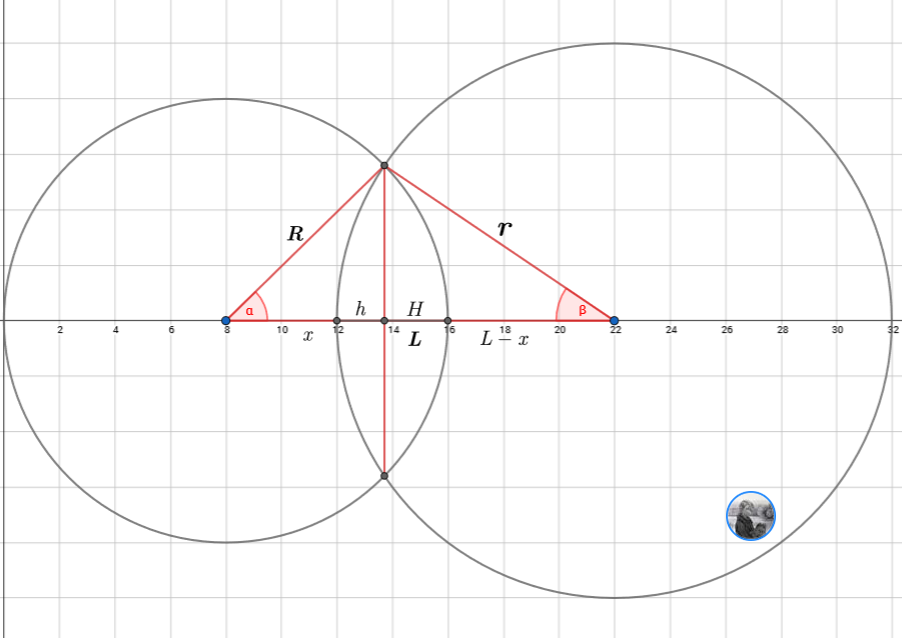
• 两个球的表面积之和减去相交部分的表面积之和
• 考虑边，然后使用球冠表面积公式$S = 2\pi RH$，答案是：$4\pi R^{2} + 4\pi r^{2} - (2\pi RH + 2\pi rh)$
• H和h为球冠的高，通过方程$R^{2} - x^{2} = r^{2} - (L-x)^{2}$求得$x$，$H = R - x$，$h = r - (L - x)$
• 考虑点，根据余弦公式求$cos\alpha = \frac{R^{2}+L^{2}-r^{2}}{2RL}$，表面积为$2\pi R^{2}(cos \alpha + 1) $，同理可得$cos\beta = \frac{r^{2}+L^{2}-R^{2}}{2rL}$，表面积为$2\pi r^{2}(cos \beta + 1) $，结果为两者之和
• 左边的球贡献的表面积为$ {\int_{\alpha}^{\pi}}2\pi Rsin\theta \sqrt{R^{2}(sin^{2}\theta+cos^{2}\theta)}d\theta = 2\pi R^{2}(cos \alpha + 1) $，右边同理

代码

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const double pi = acos(-1.0);

double squ(int x)
{
    return 1.0 * x * x;
}

double area(int R, int r, int L)
{

    double a = (squ(R) + squ(L) - squ(r)) / (2.0 * R * L);
    double b = (squ(r) + squ(L) - squ(R)) / (2.0 * r * L);
    double ans = 2 * pi * (squ(R) * (a + 1) + squ(r) * (b + 1));
    return ans;
}

int main()
{
    int R, r, L;
    while (~scanf("%d%d%d", &R, &r, &L))
    {
        double ans = area(R, r, L);
        printf("%.10f\n", ans);
    }
    return 0;
}

C. GSS and Bubble Sort

• time limit per test：1 second
• memory limit per test：512 megabytes
• input：standard input
• output：standard output

Do you remember the problem "Time Limit Exceeded" last year? Here is the code GSS wrote in that problem.

#include <stdio.h>
int main() {
  int n;
  int *vec;
  scanf("  vec = malloc(sizeof(int) * n);
  for (int i = 0; i < n; i++) {
    int t;
    scanf("%d", &t);
    vec[i] = t;
  }
  for (int i = 0; i < n; i++)
    for (int j = 0; j < n - 1; j++)
      if (vec[j] > vec[j+1])
        swap(vec[j], vec[j+1]);
  /* some other code takes O(1) time */
  return 0;
}

As you are GSS's team mate, your task is to calculate the expected time the code will run with an input of size (n), ((0< n < 10^9)). The time is measured by how many times the function swap is called. You should note that the input is a permutation of ({1,2, ..., n}) in the original problem.

Input

Input contains multiple (about 1000) test cases, please process to the end of input.

Each test cases contains an integer (n) as described above.

Output

For each test case, output one line with the answer.

If your answer is (p / q), then you should output $p × q^{10^{9}+5} $ module 1000000007 (($10^{9}+7$)).

Example

1
2

0
500000004

Note

In the second sample, there are two possible input ({1,2}) and ({2,1}), so the expected time the function swap is called is ((0 + 1) / 2 = 1/2), and $1 × 2^{10^{9} + 5}$ module ($10^{9}+7$) is (500000004).

题意

给定一个数n，组成从1,2, ...到n共n个数构成的全排列序列，求对这些序列进行冒泡排序所需交换次数的期望。

题解

n高达$10^{9}$，肯定不能暴力计算，所以将求排序过程中交换次数的期望转化为求逆序对数量的期望。而由1...n共n个数构成的全排列的逆序对的期望是$ \frac{n(n-1)}{4}$，最后结果按照要求取模即可。

结果是怎么来的呢？有一种巧妙的推导方法叫指示器随机变量，它为概率和期望之间的转换提供了一个便利的方法。以逆序对的期望数为例：

将期望分解为每一个具体的事件：共有$ C_{n}^{2}$对数，每对数为逆序对的概率是$\frac{1}{2}$（单个事件的期望是$\frac{1}{2}$），那么总得期望就是：$ C_{n}^{2} × \frac{1}{2} = \frac{n(n-1)}{4} $。

注意随机变量指示器怎么用，实际上就是将求一个随机变量的期望，分解到一个个具体的事件，每一个小事件的期望往往容易求，所有小事件的期望加起来就是总的期望。其实是从另一个角度看问题。

代码

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int mod = 1000000007;

ll modexp(ll a, ll b)
{
    ll res = 1;
    a = a % mod;
    while (b > 0)
    {
        if (b & 1)
            res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}

int main()
{
    ll n;
    while (cin >> n)
    {
        ll res = n * (n - 1) % mod;
        res = res * modexp(4, mod - 2) % mod;
        cout << res << "\n";
    }
    return 0;
}

D. GSS and Version Control（模拟）

• time limit per test：1 second
• memory limit per test：512 megabytes
• input：standard input
• output：standard output

GSS has invented a brand new version control system, called Gss's Interesting Theory, or Git in short. It support two basic operations:

1. Append a new commit to current version (thus made a new version)
2. Revert the state of the project of the (i)-th day.

As GSS just started a brand-new project, it is day 0 now. Every other day, GSS would upload his work (one of the two operations above) to the repository of the project.

The version control system would calculate the hash of the whole project. And the checksum of the project is the bitwise exclusive or (xor) of all the checksum of commits which is valid (not reverted) at one version.

Your task is to calculate the hash of the whole project after GSS's commit.

Input

The first line of input is a single number (n), the number of days that GSS works on the project.

Then (n) line follows, the i-th line consists of a string and an integer in the format below:

1. commit x, append a new commit to the current version, and (x) is the checksum of the commit, 0 ≤ x ≤ 109.
2. checkout k, revert the state of the project to the (k)-th day, 0 ≤ k < i.

Output

For each operation, output the hash of the project after the operation.

Example

7
commit 1
commit 2
checkout 1
checkout 0
commit 4
checkout 2
checkout 5

1
3
1
0
4
3
4

题意

Git的两种操作，提交与还原。提交时与前一天的结果异或，还原时将答案变为第k天的值。

题解

直接模拟即可。

• commit x：a[i] = a[i - 1] ^ x
• checkout x: a[i] = a[x]

代码

#include <iostream>
#include <cstdio>
#include <fstream>
#include <algorithm>
using namespace std;
const int maxn = 1000010;
int a[maxn];

int main()
{
//    freopen("data.in", "r", stdin);
//    freopen("data.out","w",stdout);
    int n, x;
    char s[10];
    while (scanf("%d", &n) == 1)
    {
        a[0] = 0;
        for (int i = 1; i <= n; ++i)
        {
            scanf("%s", s);
            scanf("%d", &x);
            if (s[1] == 'o')
                a[i] = x ^ a[i-1];
            else
                a[i] = a[x];
            printf("%d\n", a[i]);
        }
    }
    return 0;
}

F. A-maze-ing

• time limit per test：1 second
• memory limit per test：512 megabytes
• input：standard input
• output：standard output

Long long age, a wise but barbaric king made a plan to convert the arena to a maze so that he could get pleasure from watching his servant running the maze confusedly.

The structure of the arena could be abstracted into a directed connected graph comprised of n ($1 ≤ n ≤ 10^{5}$) nodes and m ($1 ≤ m ≤ 2 * 10^{5}$) edges.

The king had not decided where to set up the starting nodes and the end node.

So the king proposed a requirement.

Whichever two points u, v he chose, there existed a path from one point to the other(a path from u to v or from v to u).

Moreover, the king hoped to improve the difficulty of the game, so the number of nodes in the maze should be as large as possible.

You are only required to output the maximum number of nodes in the maze.

Input

There are two positive integers n and m in the first line.

And then m lines follow, in each line there are two positive integers u and v, describing that an edge from node u to node v.

Output

Just output one integer, the maximum size of the maze.

Example

3 2
1 2
1 3

2

题意

给定n点m边的有向图，求一个最大点集，要求点集中的任意两点u和v满足：要么u可以到达v，要么v可以到大u。

题解

通过强连通分量求解 + 缩点转化为有向无环图求最长路径。这道题原来遇见过很多次，但是一直都没做，这次是直接从网上找的板子。

代码

// 代码等我自己写了再补上

// 写好了，补上！2018-04-24

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <cstring>
#include <stack>
using namespace std;
const int maxn = 200010;
vector <int> E[maxn];
vector <int> G[maxn];
int n, m;
int tot, scc_cnt;

int dfn[maxn], low[maxn], sccno[maxn], sccnum[maxn], dp[maxn];
bool vis[maxn];
stack <int> s;

void tarjan(int x) // 求强连通分量
{
    dfn[x] = low[x] = ++tot;
    s.push(x);
    vis[x] = true;
    for (int i = 0; i < G[x].size(); ++i)
    {
        int v = G[x][i];
        if (!dfn[v])
        {
            tarjan(v);
            low[x] = min(low[x], low[v]);
        }
        else if (vis[v])
            low[x] = min(low[x], dfn[v]);
    }
    if (dfn[x] == low[x])
    {
        ++scc_cnt;
        while (1)
        {
            int u = s.top();
            s.pop();
            vis[u] = 0;
            sccno[u] = scc_cnt;
            sccnum[scc_cnt]++;
            if (u == x)
                break;
        }
    }
}

void find_scc()
{
    memset(vis, 0, sizeof(vis));
    memset(dfn, 0, sizeof(vis));
    memset(low, 0, sizeof(low));
    memset(sccno, 0, sizeof(sccno));
    memset(sccnum, 0, sizeof(sccnum));
    tot = scc_cnt = 0;
    for (int i = 0; i < n; ++i)
        if (!dfn[i])
            tarjan(i);
}

int search(int x) // dp
{
    if (dp[x] != -1)
        return dp[x];
    dp[x] = sccnum[x];
    for (int i = 0; i < E[x].size(); ++i)
    {
        int v = E[x][i];
        dp[x] = max(dp[x], search(v) + sccnum[x]);
    }
    return dp[x];
}

int main()
{
    int u, v;
    scanf("%d%d", &n, &m);
    for (int i = 0; i <= n; ++i)
    {
        G[i].clear();
        E[i].clear();
    }
    for (int i = 0; i < m; ++i)
    {
        scanf("%d%d", &u, &v);
        u--;
        v--;
        G[u].push_back(v);
    }
    find_scc();
    memset(dp, -1, sizeof(dp));
    for (int u = 0; u < n; ++u) //　缩点建图
    {
        for (int i = 0; i < G[u].size(); ++i)
        {
            int v = G[u][i];
            if (sccno[u] != sccno[v])
                E[sccno[u]].push_back(sccno[v]);
        }
    }
    int ans = 0;
    for (int i = 1; i <= scc_cnt; ++i)
        ans = max(ans, search(i));
    printf("%d\n", ans);
    return 0;
}

到现在还没补完。。

补充

别的题暂时不补了，E、G、H。

To be continued.
2018-04-17 星期二