CSU1804 有向无环图（记忆化搜索dp）

1804: 有向无环图

Time Limit: 5 Sec
Memory Limit: 128 Mb
Submitted: 1098
Solved: 460

Description

Bobo 有一个 n 个点，m 条边的有向无环图（即对于任意点 v，不存在从点 v 开始、点 v 结束的路径）。

为了方便，点用 1,2,…,n 编号。设 count(x,y) 表示点 x 到点 y 不同的路径数量（规定 count(x,x)=0），Bobo 想知道

除以 ($10^9+7$) 的余数。

其中，ai,bj 是给定的数列。

Input

输入包含不超过 15 组数据。

每组数据的第一行包含两个整数 n,m ($1≤n,m≤10^5$).

接下来 n 行的第 i 行包含两个整数$a_i,b_i (0≤a_i,b_i≤10^9)$.

最后 m 行的第 i 行包含两个整数 $u_i,v_i$，代表一条从点 ui 到 vi 的边 ($1≤u_i,v_i≤n$)。

Output

对于每组数据，输出一个整数表示要求的值。

Sample Input

3 3
1 1
1 1
1 1
1 2
1 3
2 3
2 2
1 0
0 2
1 2
1 2
2 1
500000000 0
0 500000000
1 2

Sample Output

4
4
250000014

Hint

Source

湖南省第十二届大学生计算机程序设计竞赛

链接

http://acm.csu.edu.cn/csuoj/problemset/problem?pid=1804

题解

latex公式神秘消失，

（根据题意无环图，则存在 Edge(i→k) 就一定不存在一条路径从k点到i点，所以计算dp[k]时就一定不会涉及到dp[i]）

另外，本题如果不是有向无环图而是一棵树的话，很显然，直接从树根往下dfs计算每个节点i的dp[i]即可，

但是现在有向无环图，可能出现如下情况：

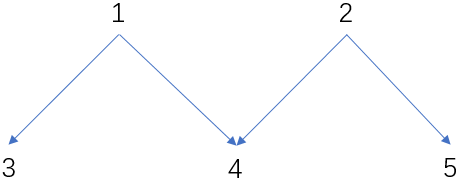
这样一来，如果主函数里单单dfs(1)或者单单dfs(2)都不能把整个图上所有节点的dp[i]都计算到，

因此要把所有in-degree[i]==0的节点i都dfs(i).

题解参考自：传送门。

dp[u]表示从u出发所能到达的所有v的count[v]*b[v]之和，每一个v都对它的前驱u有dp[v]+b[v]的贡献。

代码

Status	Accepted
Time	728ms
Memory	8272kB
Length	1481

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
typedef long long ll;
using namespace std;
const int maxn = 100010;
const int maxm = 100010;
const int mod = 1000000000 + 7;
int n, m, indegree[maxn];
ll a[maxn], b[maxn], dp[maxn];
int tot, head[maxn];

struct Edge
{
    int to, next;
}edge[maxm << 2];

void init()
{
    tot = 0;
    memset(head, -1, sizeof(head));
}

void addedge(int u, int v)
{
    edge[tot].to = v;
    edge[tot].next = head[u];
    head[u] = tot++;
}

ll dfs(int u) // 记忆化dp搜索
{
    if (dp[u] != -1) // 已经有值
        return dp[u];
    dp[u] = 0; // 初始化为0
    for (int i = head[u]; i != -1; i = edge[i].next)
    {
        int v = edge[i].to;
        dp[u] = (dp[u] + b[v] + dfs(v)) % mod; // 搜索
    }
    return dp[u];
}

int main()
{
    int u, v;
    while (scanf("%d%d", &n, &m) != EOF)
    {
        init();
        for (int i = 1; i <= n; ++i)
        {
            indegree[i] = 0;
            dp[i] = -1;
        }
        for (int i = 1; i <= n; ++i)
            scanf("%lld%lld", &a[i], &b[i]);
        for (int i = 0; i < m; ++i)
        {
            scanf("%d%d", &u, &v);
            addedge(u, v);
            indegree[v]++;
        }
        for (int i = 1; i <= n; ++i) // 从入度为0的点开始dfs
        {
            if (indegree[i] == 0)
                dfs(i);
        }
        ll ans = 0;
        for (int i = 1; i <= n; ++i)
            ans = (ans + ((dp[i] % mod) * (a[i] % mod)) % mod) % mod;
        printf("%lld\n", ans);
    }
}

The end.
2018-08-22 星期三

首先，假如我们计算 $\sum_{i=1}^{n}\sum_{j=1}^{n}count(i, j)*a_i*b_j$，这个时候，固定一个点i，枚举j进行计算的话，就有：$a_i * \Bigg(\sum_{j=1}^{n}count(i, j)*b_j \Bigg) $

我们不妨设$dp[i] = \sum_{j=1}^{n}count(i, j)*b_j$

那么，最后的 $ans = \sum_{i=1}^{n} \Bigg( a_i * \bigg(\sum_{j=1}^{n}count(i, j)*b_j \bigg) \Bigg)$ 

问题来了，状态转移方程是什么？

假设对于点i，它有K个子节点，就有：$dp[i] = \sum_{k=1}^{K}(b_k+dp[k])$