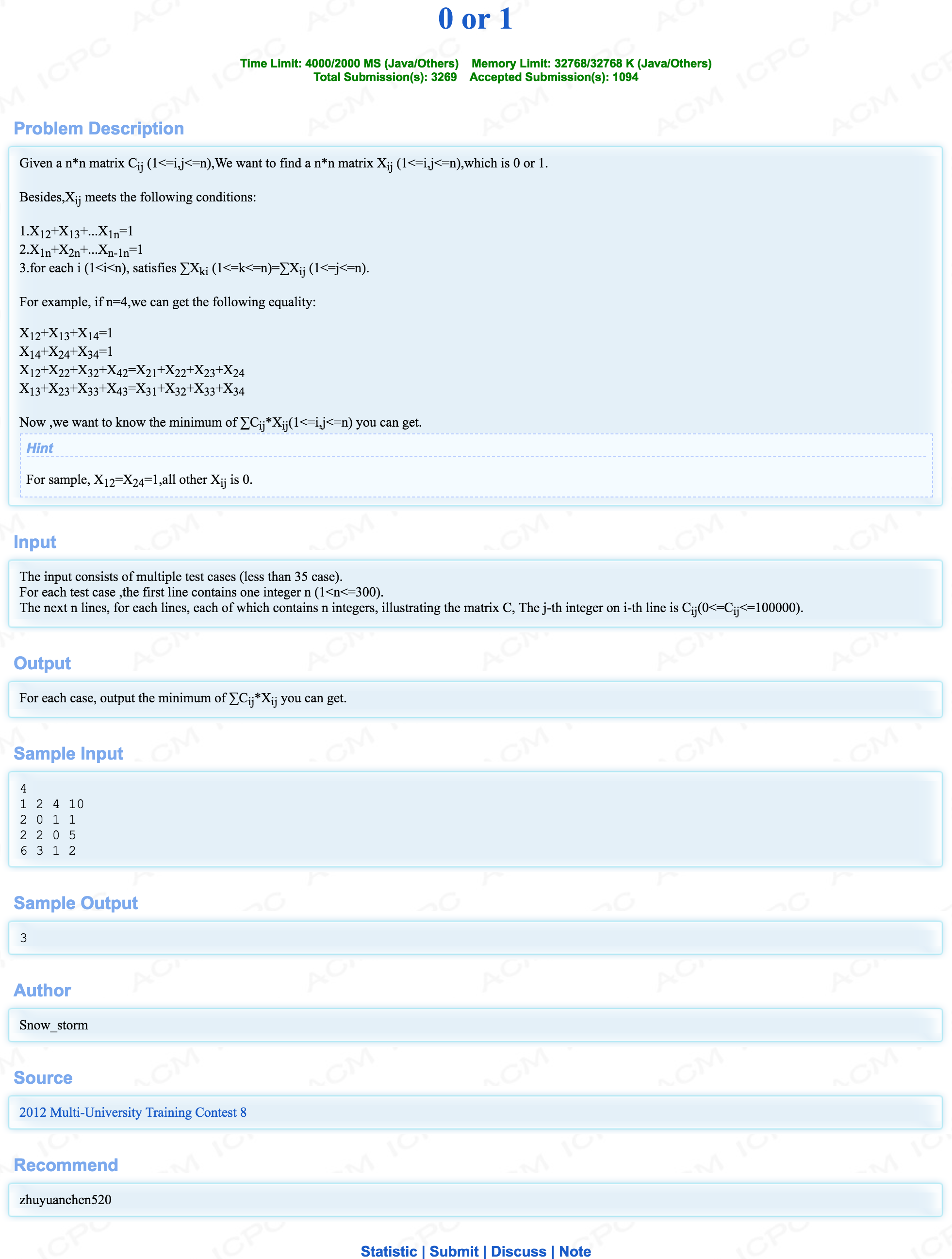
0 or 1
- Time Limit: 4000/2000 MS (Java/Others)
- Memory Limit: 32768/32768 K (Java/Others)
- Total Submission(s): 3269
- Accepted Submission(s): 1094
Sample Input
4
1 2 4 10
2 0 1 1
2 2 0 5
6 3 1 2Sample Output
3Author
Snow_storm
Source
2012 Multi-University Training Contest 8
链接
http://acm.hdu.edu.cn/showproblem.php?pid=4370
题意
给定一个n*n的矩阵C,构造一个符合以下条件的矩阵X:
- $X_{12} + X_{13} + ... + X_{1n} = 1$
- $X_{1n} + X_{2n} + ... + X_{(n-1)n} = 1$
- $\sum X_{ki} = \sum X_{ij}$ ($1 < k < n, 1 <= j <= n$)
求$\sum\limits_{i = i, j = 1}^{n} C_{ij} * X_{ij}$的最小值。
题解
将条件转化为图论最短路径问题,$X_{ij}$转化为边$i \rightarrow j$的权值,那么对应关系为:
- 表示点1的出度为1
- 表示点n的入度为1
- 除了点1和点n外的其他点出入度相等
求解的问题转化为点1到点n的一条最短路径。
其实还有一种情况,那就是可以从点1出发到达其他点然后又回到点1形成一个环,同样也可以从点n出发回到点n。这样也是符合条件的,答案为从1出发的最小权值环和从n出发的最小权值环之和。
答案为两种情况的最小值,具体可以参考bin聚的题解:传送门。
代码
代码实现的话可以使用spfa,注意最开始不是将起点s入队,而是把与起点相连的点加入队列,这样可以求得从s出发回到s的最小环,具体参考代码。
| Status | Accepted |
|---|---|
| Time | 655ms |
| Memory | 1752kB |
| Length | 1237 |
#include <bits/stdc++.h>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 310;
int G[maxn][maxn];
int dist[maxn];
bool vis[maxn];
int n;
void spfa(int s)
{
queue <int> Q;
memset(vis, false, sizeof(vis));
for (int i = 1; i <= n; ++i)
{
if (i == s) // s点初始化为inf
dist[i] = inf;
else // 与s点连边的点入队
{
dist[i] = G[s][i];
Q.push(i);
vis[i] = true;
}
}
while (!Q.empty())
{
int u = Q.front();
Q.pop();
for (int i = 1; i <= n; ++i)
{
if (dist[i] > dist[u] + G[u][i])
{
dist[i] = dist[u] + G[u][i];
if (!vis[i])
{
vis[i] = true;
Q.push(i);
}
}
}
vis[u] = false;
}
}
int main()
{
while (scanf("%d", &n) != EOF)
{
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
scanf("%d", &G[i][j]);
spfa(1);
int ans = dist[n], cir1 = dist[1]; // 简单最短路径,“环1”
spfa(n);
int cirn = dist[n]; // "环n"
ans = min(ans, cir1 + cirn); // "环1+环n" 与简单最短路径最小值
printf("%d\n", ans);
}
return 0;
}这题关键是如何将已知关系转化为图论的入度和出度,并且考虑两种情况。
The end.
2018-09-06 星期四