Hihocoder1176 欧拉路·一 （欧拉路判定）

欧拉路·一

• 时间限制:10000ms
• 单点时限:1000ms
• 内存限制:256MB

描述

小Hi和小Ho最近在玩一个解密类的游戏，他们需要控制角色在一片原始丛林里面探险，收集道具，并找到最后的宝藏。现在他们控制的角色来到了一个很大的湖边。湖上有N个小岛(编号1..N)，以及连接小岛的M座木桥。每座木桥上各有一个宝箱，里面似乎装着什么道具。

湖边还有一个船夫，船夫告诉主角。他可以载着主角到任意一个岛上，并且可以从任意一个岛上再载着主角回到湖边，但是主角只有一次来回的机会。同时船夫告诉主角，连接岛屿之间的木桥很脆弱，走过一次之后就会断掉。

因为不知道宝箱内有什么道具，小Hi和小Ho觉得如果能把所有的道具收集齐肯定是最好的，那么对于当前岛屿和木桥的情况，能否将所有道具收集齐呢？

举个例子，比如一个由6个小岛和8座桥组成的地图：

主角可以先到达4号小岛，然后按照4->1->2->4->5->6->3->2->5的顺序到达5号小岛，然后船夫到5号小岛将主角接回湖边。这样主角就将所有桥上的道具都收集齐了。

提示：欧拉路的判定

输入

第1行：2个正整数，N,M。分别表示岛屿数量和木桥数量。1≤N≤10,000，1≤M≤50,000

第2..M+1行：每行2个整数，u,v。表示有一座木桥连接着编号为u和编号为v的岛屿，两个岛之间可能有多座桥。1≤u,v≤N

输出

第1行：1个字符串，如果能收集齐所有的道具输出“Full”，否则输出”Part”。

样例输入

6 8
1 2
1 4
2 4
2 5
2 3
3 6
4 5
5 6

样例输出

Full

---

链接

http://hihocoder.com/problemset/problem/1176

题意

无向图欧拉路径/回路判定。

给定连通图G，若存在一条路，经过图中每边恰好一次，该条路称为欧拉路。

题解

无向图：

• 欧拉回路：所有顶点的度数均为偶数（起点和终点为同一个点）
• 欧拉路径：有且只有两个顶点的度数为奇数（起点&终点）

有向图：

• 欧拉回路：所有顶点的入度等于出度
• 欧拉路径：存在顶点u（终点）的入度比出度大1，v（起点）的出度比入度大1，其他顶点的入度等于出度。

注意需要判断图是否连通。

代码

Status	Accepted
Time	30ms
Memory	1024kB
Length	1043

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int maxn = 10010;
vector <int> G[maxn];
bool vis[maxn];
int degree[maxn];
int n, m;

void dfs(int u)
{
    vis[u] = true;
    for (int i = 0; i < G[u].size(); ++i)
    {
        int v = G[u][i];
        if (!vis[v])
            dfs(v);
    }
}

int main()
{
    int u, v, sum = 0;
    bool flag1, flag2 = true;
    scanf("%d%d", &n, &m);
    memset(vis, false, sizeof(vis));
    memset(degree, 0, sizeof(degree)); // 手误，写成vis了
    for (int i = 0; i < m; ++i)
    {
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        G[v].push_back(u);
        degree[u]++, degree[v]++;
    }
    for (int i = 1; i <= n; ++i)
    {
        if (degree[i] & 1) // 度为奇数的点的数量
            sum++;
    }
    flag1 = ((sum == 0 || sum == 2) ? true : false);
    dfs(1);
    for (int i = 1; i <= n; ++i) // 判断图是否连通
        if (!vis[i])
            flag2 = false;
    if (flag1 && flag2)
        printf("Full\n");
    else
        printf("Part\n");
    return 0;
}

---

The end.
2018-07-25 星期三

---

提示：欧拉路的判定

小Ho：好麻烦啊，是我的话就随便走几步，到没路可走不就好了么！

小Hi：那样的话，收集的道具会少很多，万一以后要用到，又得重新读档了。

小Ho：好吧，让我先想想。

<两分钟后>

小Ho：这个好像是一笔画问题哎，我们是在求一个方法能够一笔画出所有边吧?

小Hi：没错，这就是一笔画问题，不过它更正式的名字叫做欧拉路问题。其定义是

给定无孤立结点图G，若存在一条路，经过图中每边一次且仅一次，该条路称为欧拉路。

小Ho：既然有名字，那就证明这东西有解咯？

小Hi：没错，欧拉路是有判定条件的：一个无向图存在欧拉路当且仅当该图是连通的且有且只有2个点的度数是奇数，此时这两个点只能作为欧拉路径的起点和终点。

若图中没有奇数度的点，那么起点和终点一定是同一个点，这样的欧拉路叫做欧拉回路

对于任意一个点来说，从其他点到它的次数和从它到其他点的次数必然是相等的，否则就会出现出去次数和进入次数不同。若进入次数多，则该点位终点，若出去次数多则该点为起点。

对于一个无向图来说，进入和出去的次数恰好反映在度的数量上。所以奇数度的点至多只能有2个。

严格的证明的话：

若图G连通，有零个或两个奇数度结点，我们总有如下方法构造一条欧拉路：

1. 若有两个奇数度结点，则从其中的一个结点开始构造一条迹，即从v[0]出发经关联边e[1]“进入”v[1]，若v[1]的度数为偶数，则必可由v[1]再经关联边e[2]进入v[2]，如此进行下去，每边仅取一次。由于G是连通的，故必可到达另一奇数度结点停下，得到一条迹L：v[0]-e[1]-v[1]-e[2]…v[i]-e[i+1]…v[k]。若G中没有奇数度结点则从任一结点v[0]出发，用上述方法必可回到结点v[0]，得到上述一条闭迹L1。
2. 若L1通过了G的所有边，则L1就是欧拉路。
3. 若G中去掉L1后得到子图G′，则G′中每个结点度数为偶数，因为原来的图是连通的，故L1与G′至少有一个结点v[i]重合，在G′中由v[i]出发重复第一步的方法，得到闭迹L2。
4. 当L1与L2组合在一起，如果恰是G，则即得欧拉路，否则重复第三步可得到闭迹L3，以此类推直到得到一条经过图G中所有边的欧拉路。

不妨看看前面的例子：

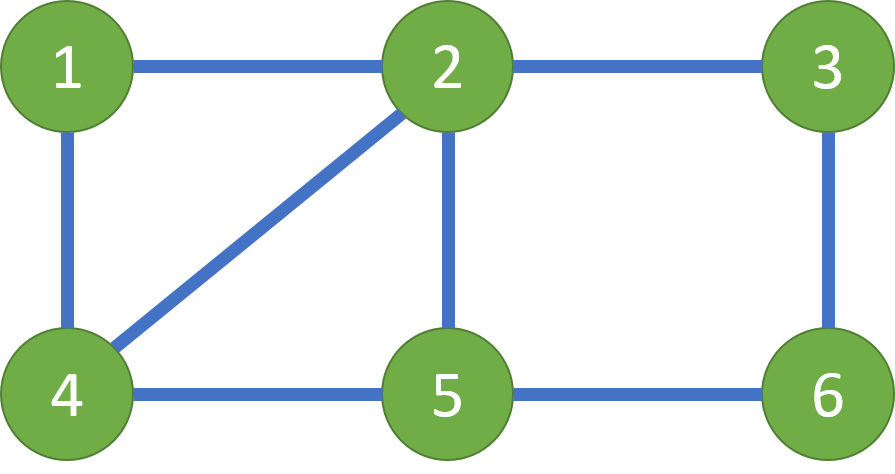
对于这个图来说，编号为4，5的点度数为奇数，其他为偶数。根据上面的性质，我们知道起点和终点一定是4、5节点。我们先从4开始随便画一条边直到无路可走：

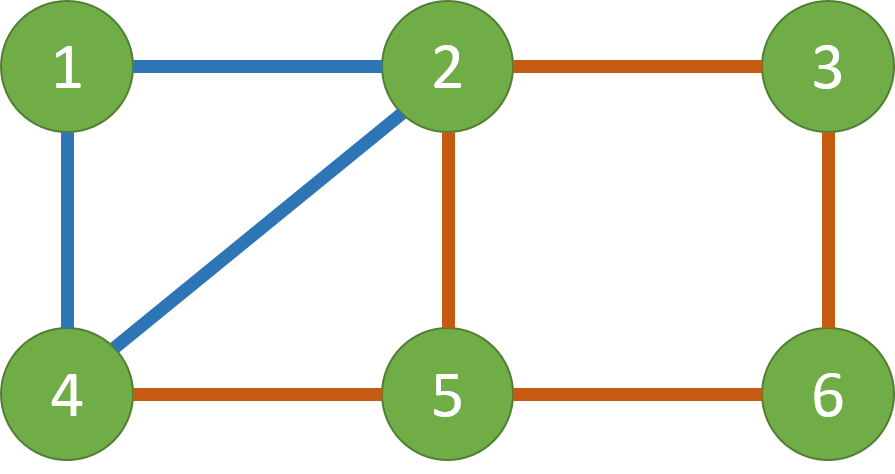
在这一步中我们连接了4-5-6-3-2-5。根据欧拉路的构造，我们得到了L1。因为L1并没有走过所有的边，所以我们执行步骤3，可以发现对于4和2都是与子图G'重合的点，在子图上我们可以得到L2(2-4-1-2)：

L1和L2合并就构成了欧拉路。

小Ho：既然有这个性质，那么我只需要计算每个点的度数就能知道能否走过所有的边了。

小Hi：没错，但是别忘了最重要的一点，需要整个图是连通的才行。