欧拉路·三
- 时间限制:10000ms
- 单点时限:1000ms
- 内存限制:256MB
描述
小Hi和小Ho破解了一道又一道难题,终于来到了最后一关。只要打开眼前的宝箱就可以通关这个游戏了。
宝箱被一种奇怪的机关锁住:
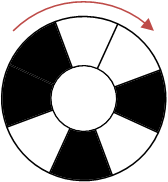
这个机关是一个圆环,一共有2^N个区域,每个区域都可以改变颜色,在黑白两种颜色之间切换。
小Ho控制主角在周围探索了一下,果然又发现了一个纸片:
机关黑色的部分表示为1,白色的部分表示为0,逆时针连续N个区域表示一个二进制数。打开机关的条件是合理调整圆环黑白两种颜色的分布,使得机关能够表示0~2^N-1所有的数字。
我尝试了很多次,终究没有办法打开,只得在此写下机关破解之法。
——By 无名的冒险者
小Ho:这什么意思啊?
小Hi:我给你举个例子,假如N=3,我们通过顺时针转动,可以使得正下方的3个区域表示为:
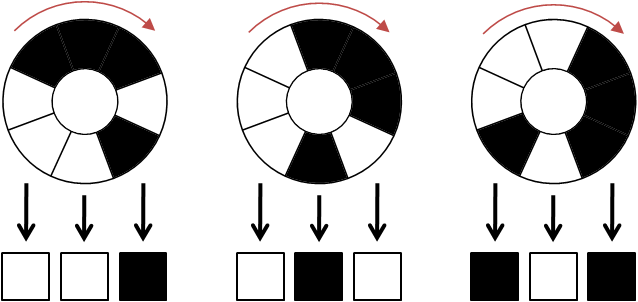
因为黑色表示为1,白色表示为0。则上面三个状态分别对应了二进制(001),(010),(101)
每转动一个区域,可以得到一个新的数字。一共可以转动2^N次,也就是2^N个数字。我们要调整黑白区域的位置,使得这2^N个数字恰好是0~2^N-1
小Ho:我懂了。若N=2,则将环上的黑白色块调整为"黑黑白白",对应了"1100"。依次是"11","10","00","01"四个数字,正好是0~3。那么这个"黑黑白白"就可以打开机关了咯?
小Hi:我想应该是的。
小Ho:好像不是很难的样子,我来试试!
输入
第1行:1个正整数,N。1≤N≤15
输出
第1行:1个长度为2^N的01串,表示一种符合要求的分布方案
样例输入
3样例输出
00010111链接
http://hihocoder.com/problemset/problem/1182
题意
描述说的很清楚了,$2^n$位二进制循环移动恰好表示从0到$2^{n-1}$共$2^n$个数。
题解
转化为欧拉回路,这个构造比较难想,提示部分讲的很清楚了。
关键是连边,我们可以将点$i(0<=i<=2^{n-1}-1)$与分别点$(i<<1)\&(2^{n-1})+0/1$相连,【左移一位是去掉最高位,和$2^{n-1}$相与是因为将前面的左移部分清零】,保存边的方式也有一点特别,具体参见代码。
代码
| Status | Accepted |
|---|---|
| Time | 21ms |
| Memory | 5120kB |
| Length | 796 |
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int maxn = 400010;
int n;
int G[maxn][2];
vector <int> V;
void init()
{
memset(G, -1, sizeof(G));
V.clear();
}
int cnt = 0;
void Euler(int u) // 欧拉回路
{
for (int i = 0; i < 2; ++i)
{
int v = G[u][i];
if (G[u][i] > -1)
{
G[u][i] = -1;
Euler(v);
}
}
V.push_back((u&1)); // 保存最后一位
}
int main()
{
int u;
scanf("%d", &u);
init();
n = (1 << (u -1)); // 点的数量
for (int i = 0; i < n; ++i)
{
int j = ((i << 1) & (n - 1)); // 建图
G[i][0] = j; // 每个点最多能连两条边,0或1
G[i][1] = j + 1;
}
Euler(0);
for (int i = V.size() - 1; i > 0; --i) // 倒序输出,最后一位顶点起点重合
printf("%d", V[i]);
printf("\n");
return 0;
}之前没有见过类似的构造,欧拉回路太神奇了。“图的可行性问题”。
The end.
2018-07-27 星期五
提示:有向图欧拉回路
< 十分钟后 >
小Ho:啊啊啊啊啊,搞不定啊!
小Hi:怎么又是这样,你怎么做的?
小Ho:是这样的,每次转动一个区域不是相当于原来数字去掉最左边一位,并在最后加上1或者0么。于是我考虑对于"XYYY",它转动之后可以变成"YYY0"或者"YYY1"。我就将所有的数字0~2^N-1看作2^N个点,连接所有的("XYYY","YYY0"),("XYYY","YYY1")。比如当N=3时,我得到了这样一个图:

我要做的就是找一条路径,从一个点出发,走过所有的点后,再回到起点。但是我发现好像很难的样子。
小Hi:那当然了。你这样构造出来的路径叫做哈密顿回路,不是那么容易可以求解的。
小Ho:哎??那我应该怎么做。
小Hi:其实你的想法是没问题的,但是需要进行一下变换。在你的构图中我们是用点来表示数字,所以需要经过每一个点。如果我们用边来表示每一个数字呢?
小Ho:怎么用边表示数字?
小Hi:其实也很简单,比如说数字"10011",分别删掉它第一个数字和最后一个数字,得到"1001","0011"。然后我们连接一条从"1001"到"0011"的有向边,表示数字"10011"。则我们可以得到构图的方法:
对于N,我们构造一个包含2^(N-1)个点和2^N条边的图,点的编号从0到2^(N-1)-1。编号为i的点表示数字i。对于任意两个点,如果点i,点j满足点i的后n-2个数字和点j的前n-2个数字相同,则我们连接有向边(i,j)。而边(i,j)表示了数字((i << 1)+(j & 1))。比如对于N=3的时候,我们可以得到:
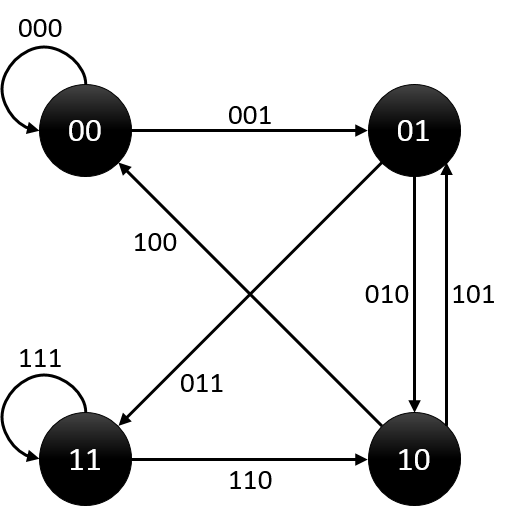
可以很容易证明对于任意不同边(i,j),其表示的数字一定不同。
小Ho:这样构图话,只要找到一条欧拉回路就可以了。但是一定会有欧拉回路么?
小Hi:当然能了,对于有向图,其存在欧拉路的条件是,至多有两个点的入度不等于出度,且这两个点满足:其中一个点入度比出度多1,另一个点出度比入度多1。
若所有点的入度都等于出度,则一定存在欧拉回路。这可以通过和无向图欧拉路同样的方法进行构造证明。
而我们构造的图,由构造方法可以知道对于任意一个点,其入度一定为2,出度一定为2。所以它必定存在欧拉回路。
在有向图中找欧拉路的方法,也仍然可以使用Fleury算法。写成伪代码的话:
DFS(u):
While (以u为起点,且未被删除的边e(u,v))
删除边e(u,v)
DFS(v)
End
PathSize ← PathSize + 1
Path[ PathSize ] ← u
但是,有一点要注意,在使用Fleury算法计算有向图的欧拉路时,我们需要将path[]倒序输出才能得到正确的路径。
小Ho:那找到欧拉回路之后呢?
小Hi:找到欧拉回路之后只要对该条欧拉回路进行拼接就可以得到我们目标的圆盘状态了。
小Ho:好,我大概明白了。我这就来试试!