网络流三·二分图多重匹配
- 时间限制:10000ms
- 单点时限:1000ms
- 内存限制:256MB
描述
学校的秋季运动会即将开始,为了决定参赛人员,各个班又开始忙碌起来。
小Hi和小Ho作为班上的班干部,统计分配比赛选手的重任也自然交到了他们手上。
已知小Hi和小Ho所在的班级一共有N名学生(包含小Hi和小Ho),编号依次为1..N。
运动会一共有M项不同的比赛,编号为1..M。第i项比赛每个班需要派出m[i]名选手参加。
根据小Hi和小Ho的统计,编号为i的学生表示最多同时参加a[i]项比赛,并且给出他所擅长的b[i]项比赛的编号。
小Hi和小Ho希望将每个学生都安排到他所擅长的比赛项目,以增加夺冠的可能性。同时又要考虑满足每项比赛对人数的要求,当然给一个学生安排的比赛项目也不能超过他愿意参加的比赛项目数量。
根据统计的结果,小Hi和小Ho想知道能否有一个合适的安排,同时满足这些条件。
输入
第1行:1个整数T,表示一共有T(2≤T≤5)组数据,每组数据按如下格式给出:
第1行:2个正整数N,M。1≤N≤100,1≤M≤100。
第2行:M个整数,第i个数表示第i个项目需要的选手数量m[i]。1≤m[i]≤N。
第3..N+2行:若干整数,第i+2行表示编号为i的学生的信息。先是a[i],b[i],接下来b[i]个整数,表示其所擅长的b[i]个项目。1≤a[i]≤M
输出
第1..T行:第i行表示第i组数据能否满足要求,若能够输出"Yes",否则输出"No"。
样例输入
2
4 3
1 2 2
1 2 1 2
2 2 1 3
1 1 2
1 2 2 3
4 3
2 2 2
1 2 1 2
2 2 1 3
1 1 2
1 2 2 3样例输出
Yes
No链接
http://hihocoder.com/problemset/problem/1393
题意
求一个二分图的最大匹配。
题解
按照提示转化为网络流模型,如果求得的最大流等于需要的选手数量之和,那么输出Yes,否则输出No。
代码
| Status | Accepted |
|---|---|
| Time | 16ms |
| Memory | 1024kB |
| Length | 2679 |
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
const int maxn = 210;
int n, m;
struct Edge
{
int u, v, cap;
Edge() {}
Edge(int u, int v, int cap): u(u), v(v), cap(cap) {}
}edge[maxn*maxn];
int R, S, T;
vector <int> E[maxn]; //边集
int dis[maxn];
int current[maxn];
void addedge(int u, int v, int cap)
{
E[u].push_back(R);
edge[R++] = Edge(u, v, cap); // 正向边
E[v].push_back(R);
edge[R++] = Edge(v, u, 0); // 方向边容量为0
// 正向边下标通过异或就得到反向边下标, 2 ^ 1 == 3 ; 3 ^ 1 == 2,R从0开始
}
int bfs()
{
memset(dis, 0x3f, sizeof(dis)); // 初始化为0x3f3f3f3f
queue <int> Q;
Q.push(S);
dis[S] = 0;
while (!Q.empty())
{
int u = Q.front();
Q.pop();
for (int i = 0; i < E[u].size(); ++i)
{
Edge &e = edge[E[u][i]];
if (e.cap > 0 && dis[e.v] == 0x3f3f3f3f)
{
dis[e.v] = dis[u] + 1;
Q.push(e.v);
}
}
}
return dis[T] < 0x3f3f3f3f; // 返回是否能够到达汇点
}
int dinic(int u, int maxflow)
{
if (u == T)
return maxflow;
for (int i = current[u]; i < E[u].size(); ++i) // 当前弧优化,保存u点增广到了第几条边
{
current[u] = i;
Edge &e = edge[E[u][i]];
if (dis[e.v] == dis[u] + 1 && e.cap > 0)
{
int flow = dinic(e.v, min(maxflow, e.cap));
if (flow)
{
e.cap -= flow; // 正向边流量减少
edge[E[u][i] ^ 1].cap += flow; // 方向边流量增加
return flow;
}
}
}
return 0;
}
int DINIC()
{
int ans = 0;
while (bfs())
{
int flow;
memset(current, 0, sizeof(current)); // bfs后清空当前弧数组
while (flow = dinic(S, 0x3f3f3f3f)) // 一次bfs可以进行多次增广
ans += flow;
}
return ans;
}
int main()
{
int t, u, cap, k;
scanf("%d", &t);
while (t--)
{
scanf("%d%d", &n, &m);
R = 0, S = 0, T = n + m + 1; // 边序号,源点,汇点
for (int i = 0; i <= T; ++i)
E[i].clear();
memset(edge, 0, sizeof(edge));
int sum = 0;
for (int i = 1; i <= m; ++i)
{
scanf("%d", &cap);
sum += cap;
addedge(n + i, T, cap);
}
for (int i = 1; i <= n; ++i)
{
scanf("%d%d", &cap, &k);
addedge(S, i, cap);
for (int j = 0; j < k; ++j)
{
scanf("%d", &u);
addedge(i, n + u, 1);
}
}
if (DINIC() == sum) // 符合要求
printf("Yes\n");
else
printf("No\n");
}
return 0;
}The end.
2018-08-01 星期三
提示:二分图多重匹配
小Ho:真是麻烦啊,要不让他们自己报名项目怎么样?
小Hi:那样可能满足不了人数的要求啊,还是根据他们的意愿来进行分配吧。
小Ho:要是每个项目都只要派一个人参加就好了。这样只需要一个简单的二分图匹配就可以决定了!
小Hi:但是现在的情况是一个人可以参加多个项目,一个项目也需要多个人参加才行。
小Ho:对啊,所以这就问题所在啊。小Hi你有什么解决的办法么?
小Hi:嗯......有了!
小Ho:什么办法?
小Hi:还是从你刚刚说的二分图匹配入手,我们仍然将学生看作A部,比赛项目看作B部:

接下来,根据每个学生的意愿我们将对应的A[i]和B[j]连起来。比如编号为i的学生擅长编号为j的项目,那么就连接A[i]-B[j]:
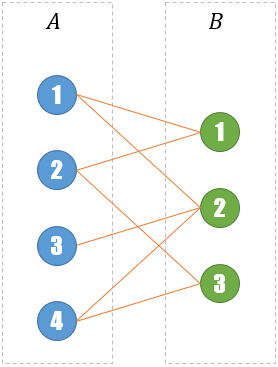
小Ho:然后呢?
小Hi:这次的问题和二分匹配不同的地方在于:匹配结果中,A[i]可能和多个B[j]相连,如果有一个可以来记录A[i]连接数量的量呢?
小Ho:记录A[i]的连接数量么?
小Hi:对!因为A[i]最多只能和a[i]的点相连。所以我们需要一个方法来限制这个量在0~a[i]之间变动。
小Ho:这听上去有点像网络流里面的流量,只能在0和容量之间变动。
小Hi:没错!这里我们要用的就是网络流。
小Ho:那具体怎么做呢?
小Hi:我们需要对之前的二分图进行进一步扩展。首先虚拟一个源点s和汇点t:
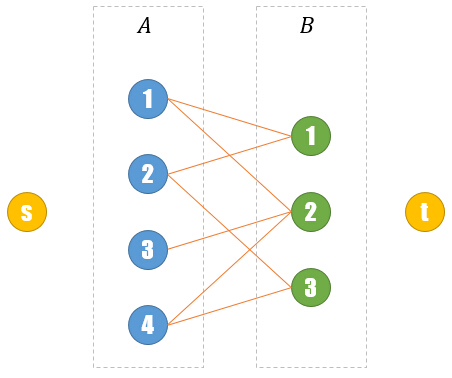
接下来我们根据a[i],在s和A[i]之间连接一条容量为a[i]的边。
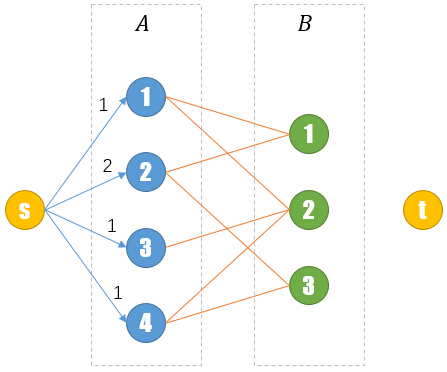
同时将原来A[i]-B[j]直接的边都改造为从A[i]到B[j]的容量为1的边。

最后我们还要连接所有的B[j]-t。由于比赛项目B[j]最多只需要m[j]名选手参加,所以我们不妨限制B[j]-t的容量为m[j]。
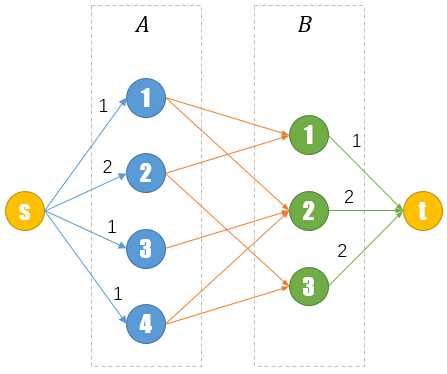
这就是我们最后的网络流图。那么小Ho,你想想在这个图上面做的最大流有什么含义?
小Ho:我想想啊......我知道了!
在完成最大流后,这个网络流图的流量情况直接对应了一个分配方案:
s-A[i]:这一类边的流量表示了A[i]参加的项目数量。
A[i]-B[j]:这一类边的流量表示了A[i]是否参加项目B[j],若参加则流量为1,否则流量为0。
B[j]-t:这一类边的流量表示了参加比赛项目B[j]的选手数量。
由于流网络会自动调整去满足最大流量,所以它会自动调整每个A[i]-B[j]的流量来使得B[j]-t尽可能大。
若每个项目都能够满足人数的话,网络流会自己调整为所有B[j]-t都满流的情况。
小Hi:就是这样,我们只需要最后判断一下每一条B[j]-t的边是否满流,就可以知道能否满足需求。同时还可以根据A[i]-B[j]的情况,计算出每个选手所参加的比赛项目。
小Ho:这个方法好厉害,都不需要自己手动去进行调整了。
小Hi:没错,这也就是网络流的神奇之处。对于这类允许多条边的匹配问题,也被称为二分图多重匹配问题。而网络流正是它的一个简单解决方法。
小Ho:我明白了!我这就去实现它,然后赶紧把报名表交上去!