HUNNU11564 Easy Delete（二分图匹配/最小点覆盖+离散化）

Easy Delete

Time Limit: 1500ms, Special Time Limit:2500ms,
Memory Limit:65536KB
Total submit users: 7
Accepted users: 4

Problem description

huicpc0215 has downloaded a lots of files in his desktop. Since there are too many files in the desktop, he wants to delete some files in the desktop. But some files can’t be deleted.

$$Figure 1 Messy Desktop$$
Each time he can choose one row or column to delete. But attention he can’t choose one row or column that has a file which can’t be deleted. Given the position of all files, please get the minimum steps for huicpc0215 to delete all files that he wants to delete.

Input

There are multiple test cases. Each test case containing:
The first line contains one integer: N (1 <= N <= 1000) , N lines follows. Each line contains three integers: F (0 <= F <= 1), X ($-1e^9 <= V <= 1e^9$), Y ($-1e^9 <= V <= 1e^9$). F=0 means this file can’t be delete. F =1 means this file must be deleted. And X and Y are the position of the file in the desktop.

Output

If huicpc0215 can achieve his goal, print minimum steps to achieve his goal, otherwise print “Sorry” in one line.

Sample Input

Sample Output

1
Sorry
2

Problem Source

2014哈尔滨理工大学秋季训练赛

链接

http://acm.hunnu.edu.cn/online/?action=problem&type=show&id=11564

题意

给定一些点的坐标，以及必须删除和不能删除的标志（1删0不删）。每次可以删除一行或者一列，问删除掉所有必须删除的点至少需要删除多少次（行+列）。如果不能完成输出Sorry。

题解

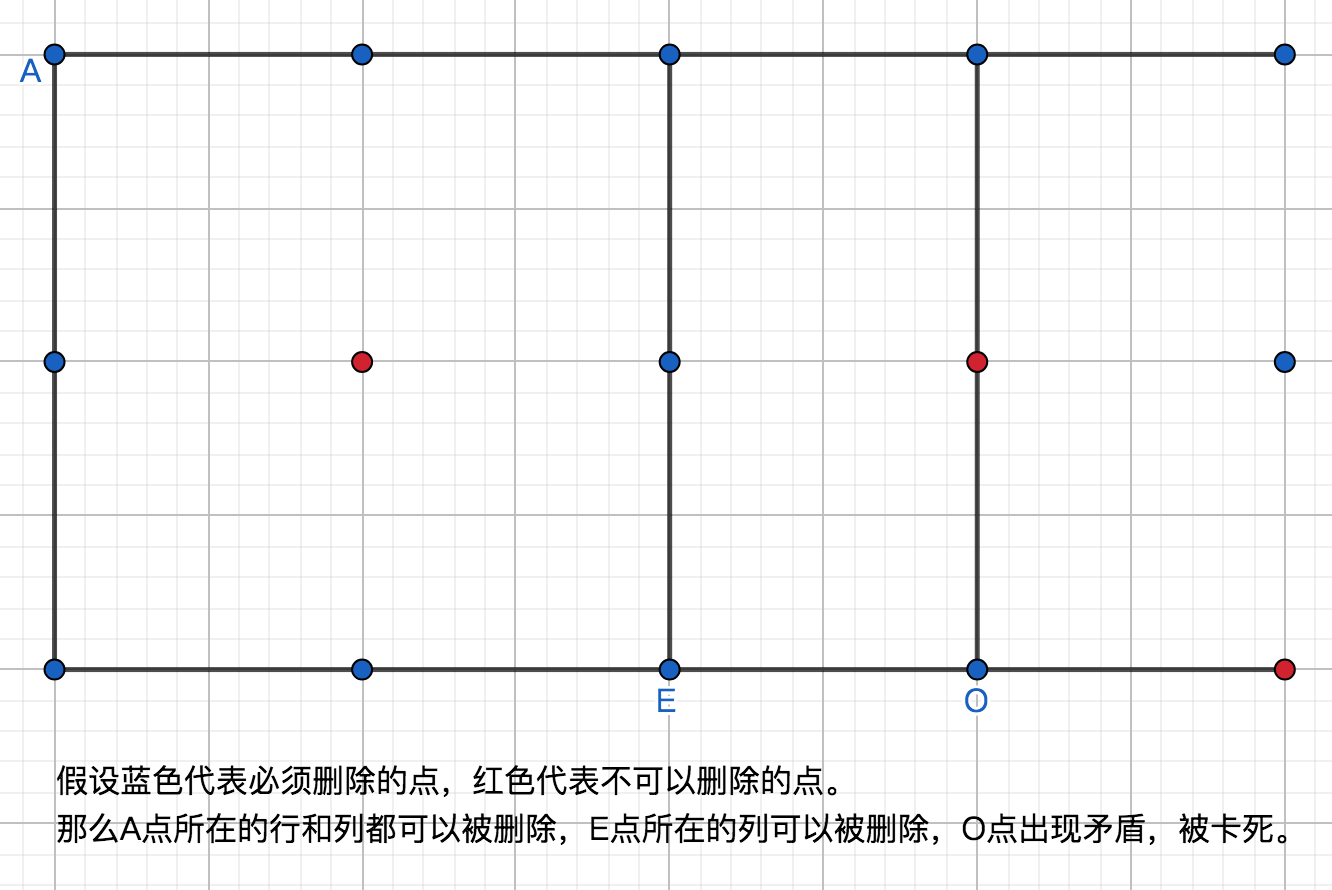
首先，不管能不能，假设所有的点都能够删除，那么我们可以建立以下模型。一个点(x,y)占据了某一行与某一列，这相当于我们把x(行)看成一个集合,y(列)看成另外一个集合，那么(x,y)这个点就是连接这两个集合的边，能够发现，这是个二分图。而要删除最少的行或者列来删除所有点，那么即求用最少的点来使覆盖所有的边，那么问题就转换成了最小顶点覆盖问题，而在二分图中， 最小顶点覆盖 = 最大匹配。模型建立好了。
而在此题中，有一些点时不可删除的，我们得做一些处理。首先点的坐标很大，得先离散化，将x和y都离散化成不同的数字，代表某一行或者某一列，然后如果该行或者该列不可以删除的话，那么就标记。然后遍历每个点，如果该点所在的行不可删除，那么我们就删除该点所在的列，将列上所有点都删除，如果是列不可删除也同理。
做完上面的工作以后，剩下的点就符合二分图的模型了，求一下最大匹配即可。

参考题解来源于：传送门。

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
const int maxn = 1010;

vector <int> gx, gy, G[maxn];
int f[maxn], x[maxn], y[maxn], a[maxn], b[maxn], sx[maxn], sy[maxn], linker[maxn], used[maxn];
int n, tot, uN;

void init()
{
    tot = 0;
    gx.clear(), gy.clear();
    memset(sx, 0, sizeof(sx)); // 标记所在行是否能够删除
    memset(sy, 0, sizeof(sy)); // 标记所在列是否能够删除
    memset(a, 0, sizeof(a)); // 标记需要单独删除的行
    memset(b, 0, sizeof(b)); // 标记需要单独删除的列
    for (int i = 0; i <= n; ++i)
        G[i].clear();
}

bool dfs(int u) // 递归寻找匹配
{
    for (int i = 0; i < G[u].size(); ++i)
    {
        int v = G[u][i];
        if (!used[v])
        {
            used[v] = true;
            if (linker[v] == -1 || dfs(linker[v]))
            {
                linker[v] = u;
                return true;
            }
        }
    }
    return false;
}

int solve() // 二分图匹配
{
    int res = 0;
    uN = gx.size();
    memset(linker, -1, sizeof(linker));
    for (int u = 1; u <= uN; ++u)
    {
        memset(used, 0, sizeof(used));
        if (dfs(u))
            ++res;
    }
    return res;
}

int main()
{
    while (scanf("%d", &n) != EOF)
    {
        init();
        for (int i = 1; i <= n; ++i)
        {
            scanf("%d%d%d", &f[i], &x[i], &y[i]);
            gx.push_back(x[i]);
            gy.push_back(y[i]);
        }
        sort(gx.begin(), gx.end()); // 排序
        sort(gy.begin(), gy.end());
        gx.erase(unique(gx.begin(), gx.end()), gx.end()); // 去重
        gy.erase(unique(gy.begin(), gy.end()), gy.end());
        for (int i = 1; i <= n; ++i) // 离散化
        {
            x[i] = lower_bound(gx.begin(), gx.end(), x[i]) - gx.begin() + 1;
            y[i] = lower_bound(gy.begin(), gy.end(), y[i]) - gy.begin() + 1;
            if (f[i] == 0) // 不可删除标记
                sx[x[i]] = sy[y[i]] = 1;
        }
        bool flag = true;
        for (int i = 1; i <= n; ++i)
        {
            if (f[i] == 0)
                continue;
            if (sx[x[i]] && sy[y[i]]) // 行和列都不可被删除，出现矛盾
            {
                flag = false;
                break;
            }
            if (sx[x[i]]) // 行不可以删除
            {
                if (b[y[i]])
                    continue;
                b[y[i]] = 1; // 删除列
                tot++;
            }
            if (sy[y[i]]) // 列不可以删除
            {
                if (a[x[i]])
                    continue;
                a[x[i]] = 1; // 删除行
                tot++;
            }
        }
        if (!flag)
        {
            printf("Sorry\n");
            continue;
        }
        for (int i = 1; i <= n; ++i)
        {
            if (f[i] == 0 || a[x[i]] || b[y[i]])
                continue;
            G[x[i]].push_back(y[i]); // 行和列都可以被删除，连边
        }
        int ans = solve() + tot;
        printf("%d\n", ans);
    }
    return 0;
}

太菜了太菜了！我的图论还没入门。

The end.
2018-08-19 星期日