LeetCodse198. House Robber（动态规划）

Easy
Accepted：302,196
Submissions：739,457

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.

Example 1:

Input: [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
             Total amount you can rob = 1 + 3 = 4.

Example 2:

Input: [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
             Total amount you can rob = 2 + 9 + 1 = 12.

链接

https://leetcode.com/problems/house-robber

题意

假设你是一个专业的抢劫犯，现在计划去偷一条街上的房子，每栋房子都藏了一定数量的钱。但是你不能偷相邻的房子，因为那样会触发警报。问你在不触发警报的情况下最多能偷多少钱。

题解

对于一栋房子我们考虑抢还是不抢，抢的话之后就不能抢相邻的房子，不抢的话就可以接着抢相邻的房子。

我们可以用递归来考虑所有的情况，假设f[0...n-1]表示抢劫0到n-1之间的房子。那么我们可以选择f[0]，然后接着从f[2]开始...

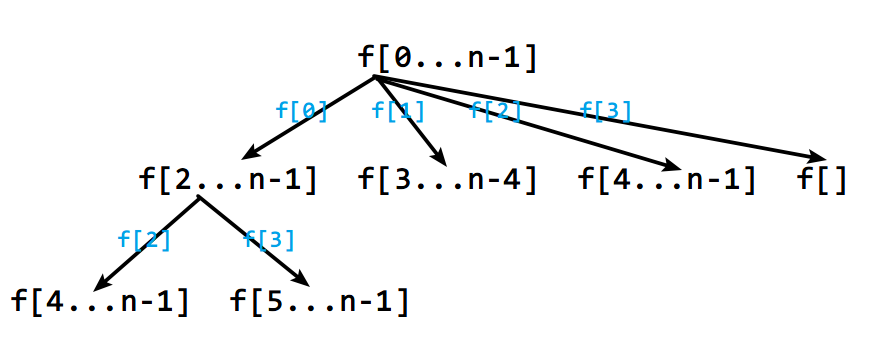
可以发现，会有很多重复的计算，所以我们可以使用自上而下的记忆化搜索（递归）或者动态规划。

动态规划使用dp[i]表示从第i栋房子到最后所抢到的最大值，那么我们可以从后往前更新：

$dp[i] = max(dp[i], nums[j] + (j + 2 < n \ ? \ dp[j + 2] : 0));$

递归时间复杂度$O(n^2)$，空间复杂度$O(n)$（使用额外数组）。

代码

Runtime: 12 ms, faster than 18.25% of C++ online submissions for House Robber.
Memory Usage: 8.6 MB, less than 100.00% of C++ online submissions for House Robber.

class Solution {
private:
    vector<int> vis;
    int solve(vector<int>& nums, int index)
    {
        if (index >= nums.size())
            return 0;
        if (vis[index] != -1)
            return vis[index];
        int res = 0;
        for (int i = index; i < nums.size(); ++i)
            res = max(res, nums[i] + solve(nums, i + 2));
        vis[index] = res;
        cout << res << endl;
        return res;
    }
    
public:
    int rob(vector<int>& nums) {
        vis = vector<int> (nums.size(), -1);
        return solve(nums, 0);
    }
};

Runtime: 4 ms, faster than 100.00% of C++ online submissions for House Robber.
Memory Usage: 8.6 MB, less than 100.00% of C++ online submissions for House Robber.

class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if (n == 0)
            return 0;
        vector<int> dp = vector<int> (n + 1, -1);
        dp[n - 1] = nums[n - 1];
        for (int i = n - 2; i >= 0; --i)
        {
            for (int j = i; j < n; ++j)
                dp[i] = max(dp[i], nums[j] + (j + 2 < n ? dp[j + 2] : 0));
        }
        return dp[0];
    }
};

Runtime: 3 ms, faster than 50.37% of C++ online submissions for House Robber.
Memory Usage: 7.7 MB, less than 45.57% of C++ online submissions for House Robber.

class Solution
{
public:
    int rob(vector<int> &nums)
    {
        n = nums.size();
        if (n == 1)
            return nums[0];
        if (n == 2)
            return max(nums[0], nums[1]);
        vector<int> dp(nums);
        dp[1] = max(nums[0], nums[1]);
        for (int i = 2; i < n; ++i)
            dp[i] = max(dp[i] + dp[i-2], dp[i-1]);
        return dp[n - 1];
    }
private:
    int n = 0;
};

The end.
2019年4月3日星期三