LeetCode343. Integer Break(动态规划)
- Medium
- Accepted:75,299
- Submissions:158,763
Given a positive integer n, break it into the sum of at least two positive integers and maximize the product of those integers. Return the maximum product you can get.
Example 1:
Input: 2
Output: 1
Explanation: 2 = 1 + 1, 1 × 1 = 1.Example 2:
Input: 10
Output: 36
Explanation: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36.Note: You may assume that n is not less than 2 and not larger than 58.
链接
https://leetcode.com/problems/integer-break
题意
给定一个正整数n,将其分解为至少两个数的和,使得这些分解的数的乘积最大。
题解
一个暴力的思路是把n所有可能的分解都求出来,然后取乘积最大值。
假设我们用f(n)表示分解n得到的乘积最大值,那么f(n) = max{1*f(n-1), 2*f(n-2), 3*f(n-3), ... , (n-1)*f(1)},比如对于f(5):
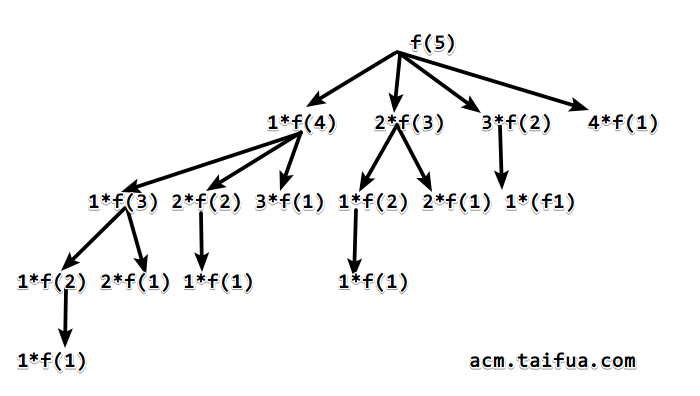
注意这种分解方法并没有考虑到n = i * (n - i)的情况,即直接分解成两个数而不是对n - i再分解,需要手动加上。
我们可以采用递归的方法来解决这个问题,但是会包含很多重复的计算,所以可以使用记忆化搜索。当然也可以直接使用动态规划。
时间复杂度$O(n^2)$。
代码
- Runtime: 4 ms, faster than 100.00% of C++ online submissions for Integer Break.
- Memory Usage: 8.5 MB, less than 19.32% of C++ online submissions for Integer Break.
class Solution {
private:
vector <int> vis;
int solve(int n)
{
if (n == 1)
return 1;
if (vis[n] != -1)
return vis[n];
int res = -1;
for (int i = 1; i < n; ++i)
res = max(max(res, i * (n - i)), i * solve(n - i));
return vis[n] = res;
}
public:
int integerBreak(int n) {
vis = vector<int>(n + 1, -1);
return solve(n);
}
};class Solution {
public:
int integerBreak(int n) {
vector <int> ans(n + 1, 1);
for (int i = 2; i <= n; ++i)
for (int j = 1; j < i; ++j)
ans[i] = max(max(ans[i], j * (i - j)), j * ans[i - j]);
return ans[n];
}
};当然还有一种数学的办法解决这个问题,只考虑因子3,具体解释见文末。
The end.
2019年3月24日 星期日
参考
The first thing we should consider is : What is the max product if we break a number N into two factors?
I use a function to express this product: f=x(N-x)
When x=N/2, we get the maximum of this function.
However, factors should be integers. Thus the maximum is (N/2)(N/2) when N is even or (N-1)/2 (N+1)/2 when N is odd.
When the maximum of f is larger than N, we should do the break.
(N/2)*(N/2)>=N, then N>=4
(N-1)/2 *(N+1)/2>=N, then N>=5
These two expressions mean that factors should be less than 4, otherwise we can do the break and get a better product. The factors in last result should be 1, 2 or 3. Obviously, 1 should be abandoned. Thus, the factors of the perfect product should be 2 or 3.
The reason why we should use 3 as many as possible is
For 6, 3 3>2 2 * 2. Thus, the optimal product should contain no more than three 2.
Below is my accepted, O(N) solution.
public class Solution {
public int integerBreak(int n) {
if(n==2) return 1;
if(n==3) return 2;
int product = 1;
while(n>4){
product*=3;
n-=3;
}
product*=n;
return product;
}
}I saw many solutions were referring to factors of 2 and 3. But why these two magic numbers? Why other factors do not work?
Let's study the math behind it.
For convenience, say n is sufficiently large and can be broken into any smaller real positive numbers. We now try to calculate which real number generates the largest product.
Assume we break n into (n / x) x's, then the product will be xn/x, and we want to maximize it.
Taking its derivative gives us n * xn/x-2 * (1 - ln(x)).
The derivative is positive when 0 < x < e, and equal to 0 when x = e, then becomes negative when x > e,
which indicates that the product increases as x increases, then reaches its maximum when x = e, then starts dropping.
This reveals the fact that if n is sufficiently large and we are allowed to break n into real numbers,
the best idea is to break it into nearly all e's.
On the other hand, if n is sufficiently large and we can only break n into integers, we should choose integers that are closer to e.
The only potential candidates are 2 and 3 since 2 < e < 3, but we will generally prefer 3 to 2. Why?
Of course, one can prove it based on the formula above, but there is a more natural way shown as follows.
6 = 2 + 2 + 2 = 3 + 3. But 2 * 2 * 2 < 3 * 3.
Therefore, if there are three 2's in the decomposition, we can replace them by two 3's to gain a larger product.
All the analysis above assumes n is significantly large. When n is small (say n <= 10), it may contain flaws.
For instance, when n = 4, we have 2 * 2 > 3 * 1.
To fix it, we keep breaking n into 3's until n gets smaller than 10, then solve the problem by brute-force.