1780: 简单的图论问题?
Description
给一个 n 行 m 列的迷宫,每个格子要么是障碍物要么是空地。每个空地里都有一个权值。你的 任务是从找一条(r1,c1)到(r2,c2)的路径,使得经过的空地的权值之和最小。每一步可以往上下 左右四个方向之一移动一格,但不能斜着移动,也不能移动到迷宫外面或者进入障碍物格子。
如下图,灰色格子代表障碍物。路径 A->B->D->F->E 的权值为 10+3+6+14+8=41,它是从 A 到 E 的最优路径。注意,如果同一个格子被经过两次,则权值也要加两次。
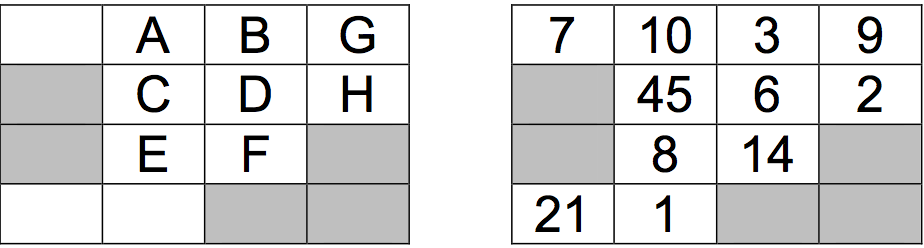
为了让题目更有趣(顺便增加一下难度),你还需要回答另外一个问题:如果你每次必须转弯 (左转、右转或者后退,只要不是沿着上次的方向继续走即可),最小权值是多少?比如,在 上图中,如果你刚刚从 A 走到 B,那么下一步你可以走到 D 或者 A,但不能走到 G。在上图 中,A 到 E 的最优路径是 A->B->D->H->D->F->E,权和为 10+3+6+2+6+14+8=49。注意,D 经 过了两次。
Input
输入包含不超过 10 组数据。每组数据第一行包含 6 个整数 n, m, r1, c1, r2, c2 (2<=n,m<=500, 1<=r1,r2<=n, 1<=c1,c2<=m). 接下来的 n 行每行包含 m 个格子的描述。每个格子要么是一个 1~100 的整数,要么是星号"*"(表示障碍物)。起点和终点保证不是障碍物。
Output
对于每组数据,输出两个整数。第一个整数是“正常问题”的答案,第二个整数是“有趣问 题”的答案。如果每个问题的答案是“无解”,对应的答案应输出-1。
Sample Input
4 4 1 2 3 2
7 10 3 9
* 45 6 2
* 8 14 *
21 1 * *
2 4 1 1 1 4
1 2 3 4
9 * * 9
2 4 1 1 1 4
1 * 3 4
9 9 * 9Sample Output
Case 1: 41 49
Case 2: 10 -1
Case 3: -1 -1Source
湖南省第十一届大学生计算机程序设计竞赛
链接
http://acm.csu.edu.cn/csuoj/problemset/problem?pid=1780
题意
n行m列的迷宫,内有障碍物,每一个格子有一个权值,现有一个起点和终点,每次可以向上下左右四个方向移动
- 问题一:问从起点到终点的最短距离(经过的所有点的最小权值和)
- 问题二:增加一个限制条件:每次移动必须改变方向,即不能沿着上次移动的方向继续移动,问从起点到终点的最短距离
题解
对于问题一:为了使权值之和尽可能小,一个格子肯定不会去走第二次,那我们只需借助优先队列进行广搜就可以了,每次取权值之和最小的位置往四个方向搜索(访问过的不再访问),直到到达目的地(r2,c2)为止对于问题二:因为要求每次都必须转弯,所以我们必须记录当前状态的前一状态是朝哪个方向走的,这样,我们这次就不能再朝这个方向走,另外,这种必须转弯的情况,一个格子最多从四个方向来访问,所以一个格子总共最多会访问4次,我们可以用数组
vis[x][y][i]表示从i这个方向是否访问过(x, y)位置(i∈[0,3])
参考了题解:传送门

官方题解说是dijkstra,第一问的话使用bfs+优先队列类似堆优化的dijkstra,但是不用松弛操作;第二问需要在第一问的基础上记录当前朝哪个方向移动这一状态,然后在转移时进行判断。至于为什么一个格子最多从四个方向来访问,看上图$D\rightarrow H$和$H\rightarrow D$就明白了(移动顺序3和4写反了)。
代码
| Status | Accepted |
|---|---|
| Time | 620ms |
| Memory | 4196kB |
| Length | 2648 |
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 510;
int G[maxn][maxn]; // 原图
int n, m, r1, c1, r2, c2;
int dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向
bool vis[maxn][maxn][4]; // 标记是否访问和从哪个方向访问该点
struct qnode
{
int x, y, val, dir; // 坐标 权值 前进方向
qnode(){}
qnode(int _x, int _y, int _val):x(_x), y(_y), val(_val){}
qnode(int _x, int _y, int _val, int _dir):x(_x), y(_y), val(_val), dir(_dir){}
bool operator < (const qnode & r) const // 权值从小到大
{
return val > r.val;
}
};
bool check(int x, int y) // 是否越界
{
return 1 <= x && x <= n && 1 <= y && y <= m;
}
int bfs1() // 问题1
{
memset(vis, 0, sizeof(vis));
qnode u, v;
priority_queue <qnode> Q;
Q.push(qnode(r1, c1, G[r1][c1])); // 入队
vis[r1][c1][0] = true; // 使用0状态表示该点已访问
while (!Q.empty())
{
u = Q.top();
Q.pop();
if (u.x == r2 && u.y == c2) // 到达终点
return u.val;
for (int i = 0; i < 4; ++i) // 四个方向前进
{
v.x = u.x + dir[i][0], v.y = u.y + dir[i][1];
if (!vis[v.x][v.y][0] && check(v.x, v.y) && G[v.x][v.y])
{
vis[v.x][v.y][0] = true;
v.val = u.val + G[v.x][v.y];
Q.push(v);
}
}
}
return -1;
}
int bfs2() // 问题2
{
memset(vis, 0, sizeof(vis));
qnode u, v;
priority_queue <qnode> Q;
Q.push(qnode(r1, c1, G[r1][c1], 4)); // 初始方向为4,实际为0123
while (!Q.empty())
{
u = Q.top();
Q.pop();
if (u.x == r2 && u.y == c2)
return u.val;
for (int i = 0; i < 4; ++i)
{
if (u.dir == i) // 该方向已访问
continue;
v.x = u.x + dir[i][0], v.y = u.y + dir[i][1];
if (!vis[v.x][v.y][i] && check(v.x, v.y) && G[v.x][v.y])
{
vis[v.x][v.y][i] = true;
v.val = u.val + G[v.x][v.y];
v.dir = i;
Q.push(v);
}
}
}
return -1;
}
int main()
{
int kase = 0;
while (scanf("%d%d%d%d%d%d", &n, &m, &r1, &c1, &r2, &c2) != EOF)
{
char s[5]; // 不超过100的整数或者字符
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
scanf("%s", s);
if (s[0] == '*')
G[i][j] = 0;
else
G[i][j] = atoi(s); // s对应的字符转为整数
}
}
printf("Case %d: %d %d\n", ++kase, bfs1(), bfs2());
}
return 0;
}The end.
2018-08-12 星期日