网络流四·最小路径覆盖
- 时间限制:10000ms
- 单点时限:1000ms
- 内存限制:256MB
描述
国庆期间正是旅游和游玩的高峰期。
小Hi和小Ho的学习小组为了研究课题,决定趁此机会派出若干个调查团去沿途查看一下H市内各个景点的游客情况。
H市一共有N个旅游景点(编号1..N),由M条单向游览路线连接。在一个景点游览完后,可以顺着游览线路前往下一个景点。
为了避免游客重复游览同一个景点,游览线路保证是没有环路的。
每一个调查团可以从任意一个景点出发,沿着计划好的游览线路依次调查,到达终点后再返回。每个景点只会有一个调查团经过,不会重复调查。
举个例子:
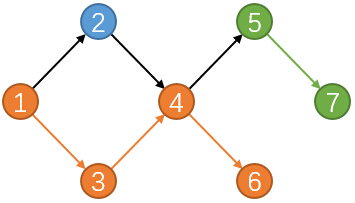
上图中一共派出了3个调查团:
- 蓝色:调查景点;2
- 橙色:调查景点;1->3->4->6
- 绿色:调查景点;5->7
当然对于这个图还有其他的规划方式,但是最少也需要3个调查团。
由于小组内的人数有限,所以大家希望调查团的数量尽可能少,同时也要将所有的景点都进行调查。
当然,如何规划调查团线路的任务落到了小Hi和小Ho的头上。
输入
第1行:2个整数N,M。1≤N≤500,0≤M≤20,000。
第2..M+1行:2个数字u,v,表示一条有向边(u,v)。保证不会出现重复的边,且不存在环。
输出
第1行:1个整数,表示最少需要的调查团数量。
样例输入
7 7
1 2
1 3
2 4
3 4
4 5
4 6
5 7样例输出
3链接
http://hihocoder.com/problemset/problem/1394
题意
求有向无环图的最小路径覆盖。
题解
拆点转化为二分图最大匹配问题,答案为n减去最大匹配。
代码
| Status | Accepted |
|---|---|
| Time | 88ms |
| Length | 983 |
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 510;
bool line[maxn][maxn];
int match[maxn];
bool vis[maxn];
int n, m;
bool find(int x)
{
for (int i = 1; i <= n; ++i)
{
if (line[x][i] && !vis[i])
{
vis[i] = true;
if (!match[i] || find(match[i]))
{
match[i] = x;
return true;
}
}
}
return false;
}
int main()
{
int ans, u, v;
while (scanf("%d%d", &n, &m) != EOF)
{
memset(line, 0, sizeof(line));
memset(match, 0, sizeof(match));
for (int i = 1; i <= m; ++i)
{
scanf("%d%d", &u, &v);
line[u][v] = 1;
}
ans = 0;
for (int i = 1; i <= n; ++i)
{
memset(vis, 0, sizeof(vis));
if (find(i))
ans++;
}
printf("%d\n", n - ans); // 点数减去最大匹配
}
return 0;
}这种二分图最大匹配是属于n点m点e条边形式的。
The end.
2018-08-01 星期三
提示:最小路径覆盖
小Ho:所以这一次我们应该如何来解决这个问题呢?
小Hi:嗯,这次的问题被称为最小路径覆盖。给定一个有向无环图,用最少的路径数量去保证所有点都被覆盖住。
小Ho:既然有名字,那一定有固定的解法了?
小Hi:没错,最小路径覆盖的结果等于N-最大二分匹配。
小Ho:二分匹配?这和二分匹配有什么关系?给定的有向图不一定是二分图吧。
小Hi:当然不是在原图上进行的二分匹配了。我们需要对原图进行转化,同时这一次我们还要学习如何用网络流去解决二分匹配的问题。
小Ho:好,你快给我讲讲。
小Hi:好的好的,你别急。我们先从例子来分析:
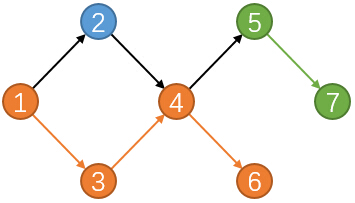
在这个例子中,我们选择的三条路径都被染上了颜色。你有发现什么特殊之处么?
小Ho:嗯...<小Ho思考了一小会儿>...并没有什么特别的地方啊?
小Hi:把黑色的边去掉,你再看看呢?主要注意的是每个点的出入度数量。
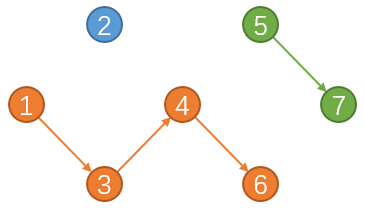
小Ho:对于一条路径,起点的入度为0,终点的出度为0,中间节点的出入度都为1。但这不是路径都应该具有的性质么?
小Hi:这个性质就是我们解决题目的关键!
每一个点最多只能有1个后继,同时每一个点最多只能有1个前驱。
假如我们选择了一条边(u,v),也就等价于把前驱u和后继v匹配上了。这样前驱u和后继v就不能和其他节点匹配。
小Ho:那就是一个前驱匹配一个后继?
小Hi:是的,利用这个我们可以这样来构图:
将每一个点拆分成2个,分别表示它作为前驱节点和后继节点。将所有的前驱节点作为A部,所有后继节点作为B部。
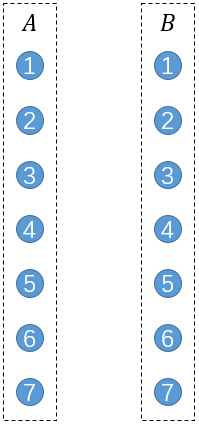
接下来进行连边,若原图中存在一条边(u,v),则连接A部的u和B部的v。
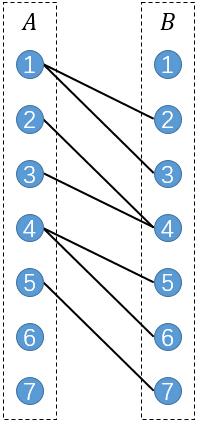
那么小Ho,你在这个上面做一个最大二分匹配怎么样?
小Ho:好!......完成了。
小Hi:不错,让我再把对应的颜色染出来:
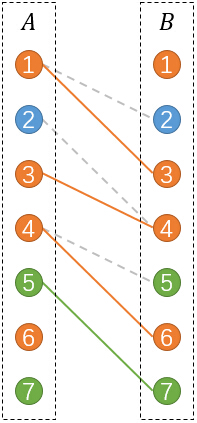
其中实线表示被选中的匹配,虚线表示未被选中的。
有没有发现,和原图刚好有着对应的关系。未被选中的匹配也正好对应了原图中我们没有选择的黑色边。
小Ho:是的呢?这是为什么呢?
小Hi:其实原理很简单。我们进行的匹配是前驱和后继的匹配。假如存在选中的匹配(i,j)和(j,k)。则表示原图中存在一条路径(i,j,k)。
比如例子中的匹配(1,3),(3,4),(4,6)就对应了原图中的路径(1,3,4,6)。
这样在匹配结束的时候,我们就可以直接通过匹配的情况来确定选中的路径。
小Ho:这个我懂了,但是如何保证这样就能得到最小的路径覆盖呢?
小Hi:你想想,每一条路径起点有什么特殊的地方?
小Ho:路径的起点入度为0...哦!我知道了。
如果一个点是路径起点的话,它在B部的节点一定是没有匹配上的。
经过最大匹配算法后,B部剩下没有被匹配的点一定是最少的,也就对应了最小需要的路径数。
所以最小路径覆盖的结果才是N-最大匹配数。
小Hi:正是这样,这样问题也就解决了。接下来第二个问题,怎么用网络流来解决二分匹配呢?
小Ho:上一次我们讲了二分多重匹配,二分匹配不就是它的简化版么。
只需要把源点s到A部的边和B部到汇点t的边容量限定为1就可以了!
小Hi:嗯,那么就只差最后一步了。
小Ho:这我也知道!实现嘛,交给我吧!