room
- 时间限制:C/C++ 1秒,其他语言2秒
- 空间限制:C/C++ 262144K,其他语言524288K
- 64bit IO Format: %lld
题目描述
Nowcoder University has 4n students and n dormitories ( Four students per dormitory). Students numbered from 1 to 4n.
And in the first year, the i-th dormitory 's students are (x1[i],x2[i],x3[i],x4[i]), now in the second year, Students need to decide who to live with.
In the second year, you get n tables such as (y1,y2,y3,y4) denote these four students want to live together.
Now you need to decide which dormitory everyone lives in to minimize the number of students who change dormitory.
输入描述
The first line has one integer n.
Then there are n lines, each line has four integers (x1,x2,x3,x4) denote these four students live together in the first year
Then there are n lines, each line has four integers (y1,y2,y3,y4) denote these four students want to live together in the second year
输出描述
Output the least number of students need to change dormitory.
输入
2
1 2 3 4
5 6 7 8
4 6 7 8
1 2 3 5输出
2说明
Just swap 4 and 5备注:
1<=n<=100
1<=x1,x2,x3,x4,y1,y2,y3,y4<=4n
It's guaranteed that no student will live in more than one dormitories.链接
https://www.nowcoder.com/acm/contest/143/E
题意
n间寝室4n个人,每间寝室住4个人。现在有些人想要更换寝室和约定好的人(一共4个)住在同一间寝室,问最少需要更换寝室的人的数量。保证同一个人不会住超过一间宿舍。
题解
建图,转化为二分图最优匹配(即带权匹配)。
我们把变化前的寝室和变化后的寝室连边,权值为不变的人的数量,那么最后的答案为总人数4*n减去最优匹配(即不变的人的数量)。
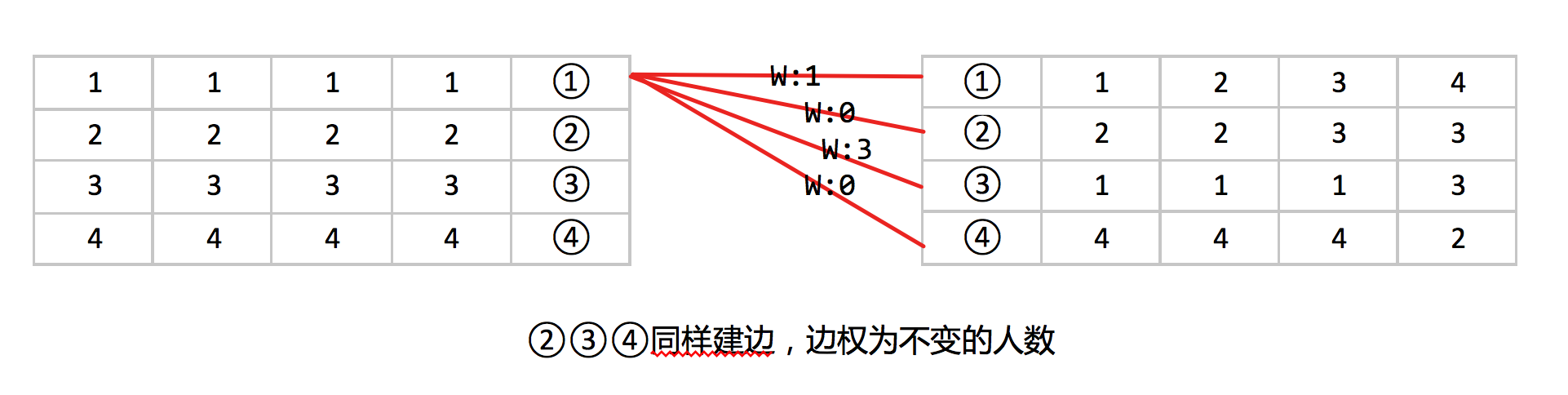
这题和队友讨论了很久,一直以为是模拟进行分类讨论,之前有想过二分图匹配,但是不知道怎么建图,最后瞎搞出来了。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 410;
const int inf = 0x3f3f3f3f;
int match[maxn], cx[maxn], cy[maxn], slack[maxn];
int G[maxn][maxn]; // 边权
bool visx[maxn], visy[maxn];
int n, nx, ny, ans;
struct Room
{
int a, b, c, d;
}rooma[maxn], roomb[maxn];
int a[410], b[410];
bool find(int x)
{
int tmp;
visx[x] = 1;
for (int y = 0; y < ny; ++y)
{
if (visy[y]) // 如果这个点已经访问过
continue;
tmp = cx[x] + cy[y] - G[x][y];
if (tmp == 0) // (x, y)在相等子图中
{
visy[y] = true;
if (match[y] == -1 || find(match[y])) // 如果这个点未匹配或者能修改
{
match[y] = x;
return true;
}
}
else if (slack[y] > tmp) // (x, y)不在相等子图中
slack[y] = tmp;
}
return false;
}
void KM()
{
for (int x = 0; x < nx; ++x) // 分别对左端点进行匹配
{
for (int i = 0; i < ny; ++i) // 初始化
slack[i] = inf;
while (true)
{
memset(visx, 0, sizeof(visx)); // 初始化,每次find()更新
memset(visy, 0, sizeof(visy));
if (find(x)) // 成功匹配后换下一个
break;
int delat = inf;
for (int i = 0; i < ny; ++i) // 计算delta值
{
if (!visy[i] && delat > slack[i])
delat = slack[i];
}
for (int i = 0; i < nx; ++i)
{
if (visx[i])
cx[i] -= delat;
}
for (int j = 0; j < ny; ++j)
{
if (visy[j])
cy[j] += delat;
else
slack[j] -= delat;
}
// 修改顶标后,要把所有的slack值都减去delta
// 这是因为lx[i] 减小了delta
// slack[j] = min(lx[i] + ly[j] -w[i][j])
}
}
}
int diff(Room x, Room y)
{
memset(a, 0, sizeof(a));
memset(b, 0, sizeof(b));
a[x.a]++, a[x.b]++, a[x.c]++, a[x.d]++;
b[y.a]++, b[y.b]++, b[y.c]++, b[y.d]++;
int ret = 0;
for (int i = 0; i < 410; ++i)
{
if (a[i] > 0 && b[i] > 0 && a[i] == b[i])
ret++;
}
return ret;
}
int main()
{
while (scanf("%d", &n) != EOF)
{
memset(G, 0, sizeof(G));
ans = 0;
nx = ny = n;
for (int i = 0; i < nx; ++i)
scanf("%d%d%d%d", &rooma[i].a, &rooma[i].b, &rooma[i].c, & rooma[i].d);
for (int i = 0; i < ny; ++i)
scanf("%d%d%d%d", &roomb[i].a, &roomb[i].b, &roomb[i].c, & roomb[i].d);
for (int i = 0; i < nx; ++i)
{
for (int j = 0; j < ny; ++j) // 边权为不变的人数
G[i][j] = diff(rooma[i], roomb[j]);
}
for (int i = 0; i < nx; ++i)
{
cx[i] = -inf;
for (int j = 0; j < ny; ++j)
{
if (cx[i] < G[i][j])
cx[i] = G[i][j];
}
}
memset(match, -1, sizeof(match));
memset(cy, 0, sizeof(cy));
KM();
for (int i = 0; i < ny; ++i)
{
if (match[i] != -1)
ans += G[match[i]][i];
}
printf("%d\n", 4*n - ans); // 总人数减去不变人数
}
return 0;
}The end.
2018-08-02 星期四