Problem I. Magic Potion
- Input file: standard input
- Output file: standard output
Description
There are n heroes and m monsters living in an island. The monsters became very vicious these days, so the heroes decided to diminish the monsters in the island. However, the i-th hero can only kill one monster belonging to the set Mi. Joe, the strategist, has k bottles of magic potion, each of which can buff one hero’s power and let him be able to kill one more monster. Since the potion is very powerful, a hero can only take at most one bottle of potion.
Please help Joe find out the maximum number of monsters that can be killed by the heroes if he uses the optimal strategy.
Input
The first line contains three integers n, m, k (1 ≤ n, m, k ≤ 500) — the number of heroes, the number of monsters and the number of bottles of potion.
Each of the next n lines contains one integer ti, the size of Mi, and the following ti integers Mi, j (1 ≤ j ≤ ti), the indices (1-based) of monsters that can be killed by the i-th hero (1 ≤ ti ≤ m, 1 ≤ Mi,j ≤ m).
Output
Print the maximum number of monsters that can be killed by the heroes.
Examples
standard input
3 5 2 4 1 2 3 5 2 2 5 2 1 2standard output
4standard input
5 10 2 2 3 10 5 1 3 4 6 10 5 3 4 6 8 9 3 1 9 10 5 1 3 6 7 10standard output
7
链接
https://codeforces.com/gym/101981
题意
n个人、m个怪兽和k瓶膜法药水,正常情况下每个人可以杀死一个怪兽,现让人服用药水,每个人至多一瓶药水,可以多杀一个怪物,问最多能杀死多少个怪兽。
题解
最大流,关键是建图。
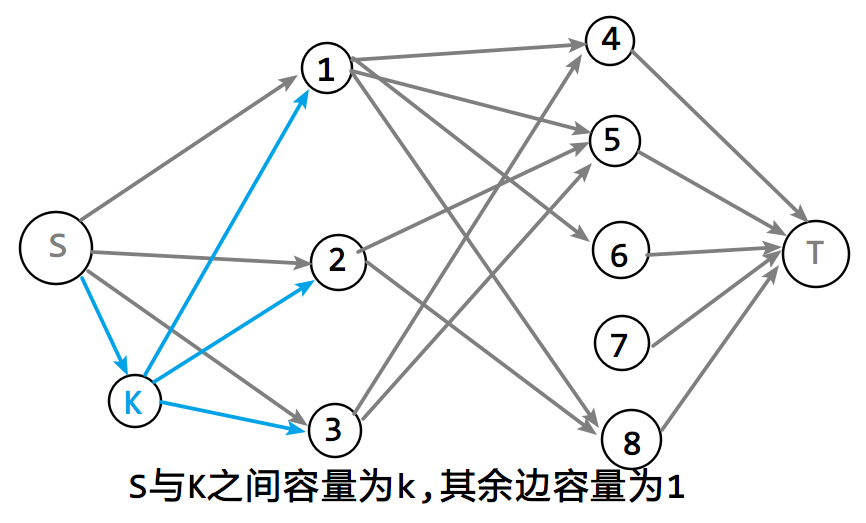
首先,每个人和怪兽之间连一条容量为1的边,起点和每个人之间连一条容量为1的边,每个怪兽和终点连一条容量为1的边。
然后处理k,对于k,我们可以再建一个点,起点和该点之间连一条容量为k的边,该点和每个人之间连一条容量为1的边。
代码
- Accepted 31 ms 12100 KB
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
const int maxn = 1010;
int n, m, k;
struct Edge
{
int u, v, cap;
Edge () {}
Edge (int _u, int _v, int _cap): u(_u), v(_v), cap(_cap) {}
}edge[maxn*maxn];
int R, S, T;
vector <int> E[maxn];
int dis[maxn];
int current[maxn];
void addedge(int u, int v, int cap)
{
E[u].push_back(R);
edge[R++] = Edge(u, v, cap);
E[v].push_back(R);
edge[R++] = Edge(v, u, 0);
}
int bfs()
{
memset(dis, 0x3f, sizeof dis);
queue <int> Q;
Q.push(S);
dis[S] = 0;
while (!Q.empty())
{
int u = Q.front();
Q.pop();
for (int i = 0; i < E[u].size(); ++i)
{
Edge &e = edge[E[u][i]];
if (e.cap > 0 && dis[e.v] == 0x3f3f3f3f)
{
dis[e.v] = dis[u] + 1;
Q.push(e.v);
}
}
}
return dis[T] < 0x3f3f3f3f;
}
int dinic(int u, int maxflow)
{
if (u == T)
return maxflow;
for (int i = current[u]; i < E[u].size(); ++i)
{
current[u] = i;
Edge &e = edge[E[u][i]];
if (dis[e.v] == dis[u] + 1 && e.cap > 0)
{
int flow = dinic(e.v, min(maxflow, e.cap));
if (flow)
{
e.cap -= flow;
edge[E[u][i]^1].cap += flow;
return flow;
}
}
}
return 0;
}
int DINIC()
{
int ans = 0;
while (bfs())
{
int flow;
memset(current, 0, sizeof current);
while (flow = dinic(S, 0x3f3f3f3f))
ans += flow;
}
return ans;
}
int main()
{
int t, u;
scanf("%d%d%d", &n, &m, &k);
R = 0;
S = 0, T = n + m + 2;
for (int i = 0; i <= T; ++i)
E[i].clear();
memset(edge, 0, sizeof edge);
for (int i = 1; i <= n; ++i) // 人与怪物之间连边
{
scanf("%d", &t);
for (int j = 1; j <= t; ++j)
{
scanf("%d", &u);
addedge(i, n + u, 1);
}
}
for (int i = 1; i <= n; ++i) // 起点与人之间连边
addedge(S, i, 1);
for (int i = 1; i <= m; ++i) // 怪物与终点之间连边
addedge(n + i, T, 1);
addedge(S, n + m + 1, k); // 新增点处理额外流量k
for (int i = 1; i <= n; ++i) // 新增点与人之间连边
addedge(n + m + 1, i, 1);
int ans = DINIC();
printf("%d\n", ans);
return 0;
}The end.
2018-11-19 星期一