牛客国庆集训派对Day3 I Metropolis（多源最短路）

Metropolis

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 524288K，其他语言1048576K
64bit IO Format: %lld

题目描述

魔方国有n座城市，编号为1到n。城市之间通过n-1条无向道路连接，形成一个树形结构。
在若干年之后，其中p座城市发展成了大都会，道路的数量也增加到了m条。
大都会之间经常有贸易往来，因此，对于每座大都会，请你求出它到离它最近的其它大都会的距离。

输入描述

第一行三个整数$n,m,p (1 ≤ n,m ≤ 2*10^5,2 ≤ p ≤ n)$，第二行p个整数表示大都会的编号 (1≤ xi≤ n)。接下来m行每行三个整数ai,bi,li表示一条连接ai和bi，长度为li的道路 ($1 ≤ ai,bi ≤ n,1 ≤ li ≤ 10^9$)。
保证图是连通的。

输出描述

输出一行p个整数，第i个整数表示xi的答案。

输入

输出

3 3 5

链接

https://ac.nowcoder.com/acm/contest/203/I?&headNav=www

题意

n个点m条边的无向带权图，求其中p个点每个点到其他p-1个点中最短距离的点的距离（好绕口啊）。

题解

考虑到数据范围，所以肯定不能跑p次最短路。但是可以把所有大都会都作为源点跑多源点最短路，记录每个点是由哪个源点扩展的，只要两个不同源点的最短路相遇，就更新两个源点的答案。

具体点讲，有如下两种情况：

p3l

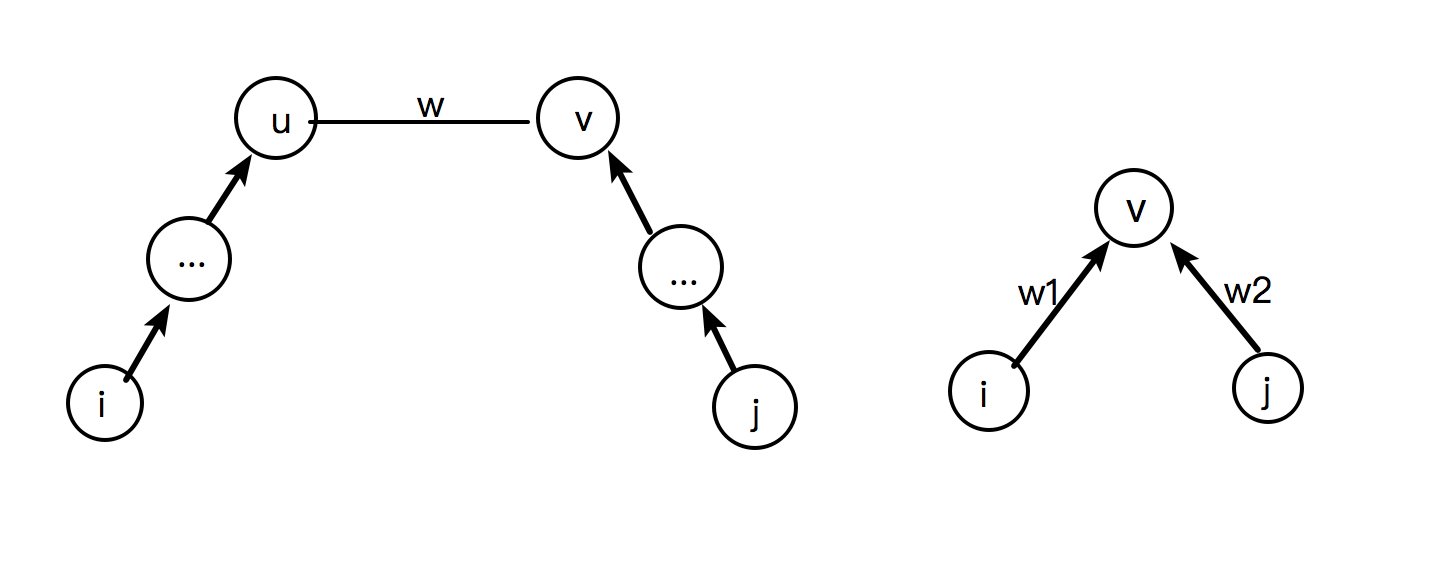
情况一：$dist(i, j) = min(dist(i, j), dist[u] + dist[v] + w)$
情况二：$dist(i, j) = d[i] + w_1 + d[v]$ 、$dist(i, j) = d[j] + w_2 + d[v]$【d[i], d[j]就相当于d[u]】

具体见代码。

代码

286ms 22876KB

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 200010;
const ll inf = 0x3f3f3f3f3f3f3f3f;

int p[maxn], from[maxn]; // from[i]记录点i是由哪个源点扩展的
ll dist[maxn], ans[maxn];
bool vis[maxn];
int n, m, k;

struct Node
{
    int v;
    ll c;
    Node(int _v, ll _c): v(_v), c(_c) {}
    bool operator < (const Node & r) const
    {
        return c > r.c;
    }
};

struct Edge
{
    int to;
    ll w;
    Edge(int _to, ll _w): to(_to), w(_w) {}
};

vector <Edge> edge[maxn];

void addedge(int u, int v, ll w)
{
    edge[u].push_back(Edge(v, w));
}

void dijkstra() // 最短路
{
    for (int i = 0; i <= n; ++i)
    {
        vis[i] = false;
        dist[i] = inf;
        ans[i] = inf;
    }
    priority_queue <Node> Q;
    for (int i = 0; i < k; ++i)
    {
        dist[p[i]] = 0;
        Q.push(Node(p[i], dist[p[i]]));
    }
    while (!Q.empty())
    {
        Node tmp = Q.top();
        Q.pop();
        int u = tmp.v;
        if (vis[u])
            continue;
        vis[u] = true;
        for (int i = 0; i < edge[u].size(); ++i)
        {
            int v = edge[u][i].to;
            ll cost = edge[u][i].w;
            if (dist[v] > dist[u] + cost) // 更新最短路
            {
                dist[v] = dist[u] + cost;
                Q.push(Node(v, dist[v]));
                from[v] = from[u];
            }
            else if (from[v] != from[u]) // u和v由不同源点扩展，则更新答案
            {
                ans[from[u]] = min(ans[from[u]], dist[u] + dist[v] + cost);
                ans[from[v]] = min(ans[from[v]], dist[v] + dist[u] + cost);
            }
        }
    }
}

int main()
{
    memset(from, 0, sizeof from);
    for (int i = 0; i <= n; ++i)
        edge[i].clear();
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i < k; ++i)
    {
        scanf("%d", &p[i]);
        from[p[i]] = p[i];
    }
    int u, v;
    ll w;
    for (int i = 0; i < m; ++i)
    {
        scanf("%d%d%lld", &u, &v, &w);
        addedge(u, v, w);
        addedge(v, u, w);
    }
    dijkstra();
    printf("%lld", ans[p[0]]);
    for (int i = 1; i < k; ++i)
        printf(" %lld", ans[p[i]]);
    printf("\n");
    return 0;
}

The end.
2018-11-16 星期五