POJ1523 SPF（Tarjan求割点）

SPF

Time Limit: 1000MS
Memory Limit: 10000K
Total Submissions: 10137
Accepted: 4541

Description

Consider the two networks shown below. Assuming that data moves around these networks only between directly connected nodes on a peer-to-peer basis, a failure of a single node, 3, in the network on the left would prevent some of the still available nodes from communicating with each other. Nodes 1 and 2 could still communicate with each other as could nodes 4 and 5, but communication between any other pairs of nodes would no longer be possible.
Node 3 is therefore a Single Point of Failure (SPF) for this network. Strictly, an SPF will be defined as any node that, if unavailable, would prevent at least one pair of available nodes from being able to communicate on what was previously a fully connected network. Note that the network on the right has no such node; there is no SPF in the network. At least two machines must fail before there are any pairs of available nodes which cannot communicate.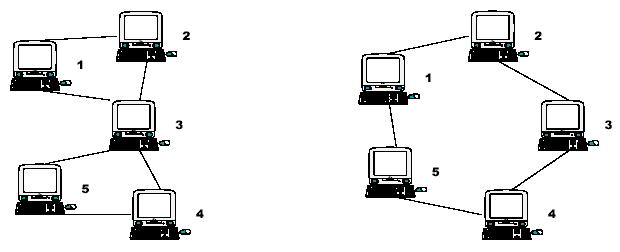

Input

The input will contain the description of several networks. A network description will consist of pairs of integers, one pair per line, that identify connected nodes. Ordering of the pairs is irrelevant; 1 2 and 2 1 specify the same connection. All node numbers will range from 1 to 1000. A line containing a single zero ends the list of connected nodes. An empty network description flags the end of the input. Blank lines in the input file should be ignored.

Output

For each network in the input, you will output its number in the file, followed by a list of any SPF nodes that exist.
The first network in the file should be identified as "Network #1", the second as "Network #2", etc. For each SPF node, output a line, formatted as shown in the examples below, that identifies the node and the number of fully connected subnets that remain when that node fails. If the network has no SPF nodes, simply output the text "No SPF nodes" instead of a list of SPF nodes.

Sample Input

Sample Output

Network #1
  SPF node 3 leaves 2 subnets

Network #2
  No SPF nodes

Network #3
  SPF node 2 leaves 2 subnets
  SPF node 3 leaves 2 subnets

Source

Greater New York 2000

链接

http://poj.org/problem?id=1523

题意

给定一个无向图，求其中的割点以及割点产生的连通分量的数量。

题解

Tarjan求割点，用cut[]数组记录产生的连通分量数量，输入和输出都需要特殊处理一下。

求出关节点u后，还有一个问题需要解决：去掉该关节点u，将原来的连通图分成了几个连通分量？
1) 如果关节点u是根结点，则有几个子女，就分成了几个连通分量；
2) 如果关节点u不是根结点，则有d个子女w ，使得low[w]>=dfn[u]，则去掉该结点，分成了d+1个连通分量。

代码

Status	Accepted
Memory	124kB
Length	2257

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>
using namespace std;
const int maxn = 1010;
int dfn[maxn], low[maxn], cut[maxn], head[maxn];
int n, m, tot, cnt, cutcnt, rootson;

struct Edge
{
    int to, next;
}edge[maxn];

void addedge(int u, int v) // 链式前向星存图
{
    edge[cnt].to = v;
    edge[cnt].next = head[u];
    head[u] = cnt++;
}

void init()
{
    tot = cutcnt = cnt = rootson = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(cut, 0, sizeof(cut));
    memset(edge, 0, sizeof(edge));
    memset(head, -1, sizeof(head));
}

void tarjan(int u, int father) // 求割点
{
    low[u] = dfn[u] = ++tot;
    for (int i = head[u]; i != -1; i = edge[i].next)
    {
        int v = edge[i].to;
        if (!dfn[v])
        {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u] && u != 1) // 判断割点条件
                cut[u]++;
            else if (u == 1) // 判断根节点的子树数量
                rootson++;
        }
        else if (v != father)
            low[u] = min(low[u], dfn[v]);
    }
}

int main()
{
//    freopen("/Users/taifu/Codes/CPP/data.in", "r", stdin);
//    freopen("/Users/taifu/Codes/CPP/data.out","w",stdout);
    int u, v, kase = 0, linenum = 1;
    while (1)
    {
        scanf("%d", &u);
        if (u == 0)
            break;
        init();
        scanf("%d", &v);
        n = u;
        n = max(n, max(u, v));
        addedge(u, v);
        addedge(v, u);
        while (1)
        {
            scanf("%d", &u);
            if (u == 0)
                break;
            scanf("%d", &v);
            n = max(n, max(u, v));
            addedge(u, v);
            addedge(v, u);
        }
        if (linenum > 1) // 输出最后呢一行没有空格
            printf("\n");
        printf("Network #%d\n", ++kase);
        linenum++;
        tarjan(1, 0);
        if (rootson > 1) // 为了方便后面加1，根节点产生的连通分量的在此减一
            cut[1] = rootson - 1;
        bool flag = false;
        for (int i = 1; i <= n; ++i)
        {
            if (cut[i] > 0)
            {
                flag = true;
                printf("  SPF node %d leaves %d subnets\n", i, cut[i] + 1);
            }
        }
        if (!flag)
            printf("  No SPF nodes\n");
    }
    return 0;
}

The end.
2018-07-17 星期二