UVA10537 The Toll! Revisited（最短路）

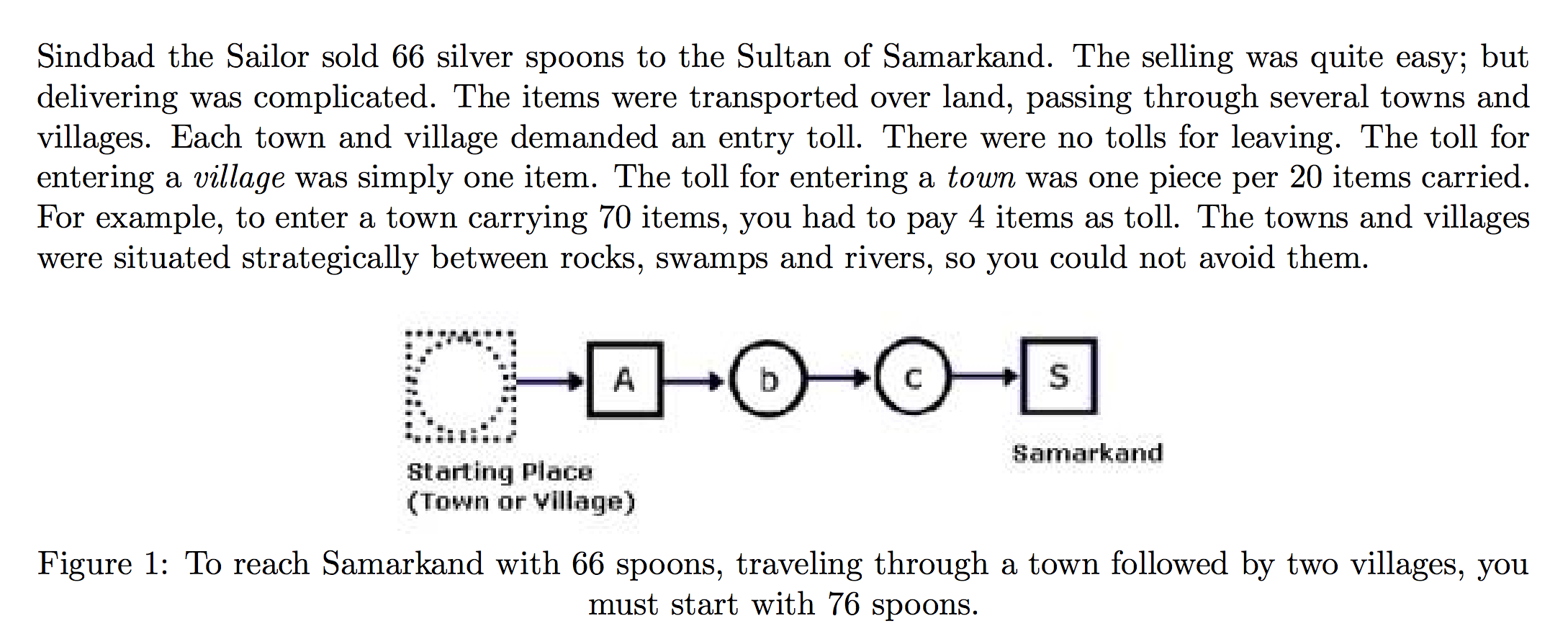
The Toll! Revisited

Input

The input consists of several test cases. Each test case consists of two parts: the roadmap followed by the delivery details.
The first line of the roadmap contains an integer n, which is the number of roads in the map
(0 ≤ n). Each of the next n lines contains exactly two letters representing the two endpoints of a road.
A capital letter represents a town; a lower case letter represents a village. Roads can be traveled in either direction.
Following the roadmap is a single line for the delivery details. This line consists of three things: an integer p (0 < p < 1000000000) for the number of items that must be delivered, a letter for the starting place, and a letter for the place of delivery. The roadmap is always such that the items can be delivered.
The last test case is followed by a line containing the number ‘-1’.

Output

The output consists of three lines for each test case. First line displays the case number, second line
shows the number of items required at the beginning of the journey and third line shows the path
according to the problem statement above. Actually, the path contains all the city/village names that
Sindbad sees along his journey. Two consecutive city/village names in the path are separated by a
hyphen.

Sample Input

1
a Z
19 a Z
5
A D
D X
A b
b c
c X
39 A X
-1

Sample Output

Case 1:
20
a-Z
Case 2:
44
A-b-c-X

---

链接

https://cn.vjudge.net/problem/UVA-10537

题意

运送货物需要缴纳过路费。进入一个村庄需要缴纳一单位的货物，而进入一个城镇时，每20个单位的货物中就要上缴一个单位(70 = 20 + 20 + 20 + 10 = 1 + 1 + 1 + 1 = 4)。现给定一个起点和终点，输出一条缴纳过路费最少的路线，有多条路线时输出字典序最小的。

题解

尽管和普通的最短路不尽相同，本题仍然可以用Dijkstra算法的思路解决，所不同的是需进行逆推而非顺推。令d[i]表示进入节点i之后，至少要有d[i]单位的货物，到达目的地时货物数量才足够，则每次选择一个d[i]最小的未标号结点，更新它的所有前驱结点的d值即可算出所有的d值，然后在输出路径时根据d值可以直接构造字典序最小解。需要注意的是，d[i]可能会超过无符号32位证书的范围，需要用long long。

——小白书P332

本题的坑点除了long long外，还需注意到达城镇u时，下一个点v至少需要多少货物。假设我们到达u时至少需要100，那么按照100计算的话，在点u处需要缴纳5的过路费，即d[u] = 100，d[v] = 105，实际上从v到u时，需要缴纳105(1+1+1+1+1+1=6)的过路费，因为那个过路费5也需要缴纳1过路费。所以实际计算的时候不能用20来算，我们看有多少个19，就缴纳多少的过路费。即$d[v] = d[u] + \frac{d[u]+18}{19}$。如果是村庄的话那么$d[v] = d[u] + 1$就行了。

需要详细的说明可以参考博客：传送门。

代码

Status	Accepted
Length	2538

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
#include <vector>
using namespace std;
typedef long long ll;
const long long inf = (1ll << 62);
const int maxn = 110;
const int maxm = 1010;
ll dist[maxn], D;
bool vis[maxn];
int n, pre[maxn];

struct Node
{
    int v;
    ll dis;
    Node(int _v, ll _dis): v(_v), dis(_dis) {}
    bool operator < (const Node & r) const
    {
        return dis > r.dis;
    }
};

struct Edge
{
    int to, cost;
    Edge(int _to): to(_to) {}
    Edge(int _to, int _cost): to(_to), cost(_cost) {}
};

vector <Edge> edge[maxn];

void addedge(int u, int v)
{
    edge[u].push_back(Edge(v));
}

int char2int(char ch) // 字母转数字
{
    return ch - 'A';
}

char int2char(int x) // 数字转字母
{
    return char(x + 65);
}

ll Cost(int u) // 到达点u时下一个点v的花费
{
    if (u < 26) // 大写字母-城镇
        return dist[u] + (dist[u] + 18) / 19;
    return dist[u] + 1; // 村庄
}

void dijkstra(int s)
{
    for (int i = 0; i < maxn; ++i) // 点数，不为n
    {
        dist[i] = inf;
        vis[i] = false;
        pre[i] = -1;
    }
    dist[s] = D;
    priority_queue <Node> Q;
    Q.push(Node(s, dist[s]));
    while (!Q.empty())
    {
        Node tmp = Q.top();
        Q.pop();
        int u = tmp.v;
        if (vis[u])
            continue;
        vis[u] = true;
        for (int i = 0; i < edge[u].size(); ++i)
        {
            int v = edge[u][i].to;
            if (vis[v])
                continue;
            ll cost = Cost(u);
            if (dist[v] > cost) // 更新到达v点所需要的最少货物
            {
                pre[v] = u; // 记录前驱节点
                dist[v] = cost;
                Q.push(Node(v, dist[v]));
            }
            else if (dist[v] == cost && u < pre[v]) // 相等时取字典序最小的
                pre[v] = u;
        }
    }
}

int main()
{
    int s, t, kase = 0;
    char s1[2], s2[2];
    while (scanf("%d", &n))
    {
        if (n == -1)
            break;
        for (int i = 0; i < maxn; ++i) // 注意点的范围
            edge[i].clear();
        for (int i = 1; i <= n; ++i)
        {
            scanf("%s%s", s1, s2);
            addedge(char2int(s1[0]), char2int(s2[0]));
            addedge(char2int(s2[0]), char2int(s1[0]));
        }
        scanf("%lld%s%s", &D, s1, s2);
        s =  char2int(s1[0]), t = char2int(s2[0]);
        dijkstra(t); // 从终点开始逆序求最短路
        printf("Case %d:\n", ++kase);
        printf("%lld\n", dist[s]);
        while (pre[s] != -1) // 逆序输出
        {
            printf("%c-", int2char(s));
            s = pre[s];
        }
        printf("%c\n", int2char(t));
    }
    return 0;
}

之前不知道long long inf = 1<<30会爆精度，实际上要用long long inf = 1ll<<30，然后由于数组初始化又错了一次，数组的范围并不是n。

---

The end.
2018-08-24 星期五