UVA1411 Ants（二分图最优匹配/最小权值匹配）

Ants

Time Limit: 5000MS	Memory Limit: 65536K
Total Submissions: 7479	Accepted: 2368

Description

Young naturalist Bill studies ants in school. His ants feed on plant-louses that live on apple trees. Each ant colony needs its own apple tree to feed itself.

Bill has a map with coordinates of n ant colonies and n apple trees. He knows that ants travel from their colony to their feeding places and back using chemically tagged routes. The routes cannot intersect each other or ants will get confused and get to the wrong colony or tree, thus spurring a war between colonies.

Bill would like to connect each ant colony to a single apple tree so that all n routes are non-intersecting straight lines. In this problem such connection is always possible. Your task is to write a program that finds such connection.

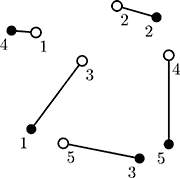
On this picture ant colonies are denoted by empty circles and apple trees are denoted by filled circles. One possible connection is denoted by lines.

Input

The first line of the input file contains a single integer number n (1 ≤ n ≤ 100) — the number of ant colonies and apple trees. It is followed by n lines describing n ant colonies, followed by n lines describing n apple trees. Each ant colony and apple tree is described by a pair of integer coordinates x and y (−10 000 ≤ x, y ≤ 10 000) on a Cartesian plane. All ant colonies and apple trees occupy distinct points on a plane. No three points are on the same line.

Output

Write to the output file n lines with one integer number on each line. The number written on i-th line denotes the number (from 1 to n) of the apple tree that is connected to the i-th ant colony.

Sample Input

Sample Output

Source

Northeastern Europe 2007

链接

https://vjudge.net/problem/UVA-1411

题意

给出n个白点和n个黑点的坐标，要求用n条不相交的线段把它们连接起来，其中每条线段恰好连接一个白点和一个黑点，每个点恰好连接到一条线段。

题解

因为结点有黑白两色，我们不难想到构造一个二分图，其中每个白点对应一个X结点，每个黑点对应一个Y结点，每个黑点和每个白点相连，权值等于二者的欧几里得距离的相反数，跑一遍二分图最大权值匹配就能得到答案。
假设在匹配中有$a_1-b_1$和$a_2-b_2$相交，那么$dist(a_1, b_1)+dist(a_2,b_2)$一定大于$dist(a_1, b_2)+dist(a_2,b_1)$，因此如果把这两条线段改成$a_1-b_2$和$a_2-b_1$后总长度会变小，与“最大权值”矛盾，所以我们实际上求的是是二分图最小权值匹配，匹配中不会出现线段相交的情况。

代码

Status	Accepted
Time	30ms
Length	2697

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <vector>
using namespace std;
const int maxn = 110;
const double inf = 0x3f3f3f3f * 1.0;
int nx, ny, n;
double G[maxn][maxn], lx[maxn], ly[maxn], slack[maxn];
int linker[maxn];
bool visx[maxn], visy[maxn];

bool eq(double a, double b)
{
    return fabs(a - b) < 1e-9;
}

bool dfs(int x)
{
    visx[x] = true;
    for (int y = 0; y < ny; ++y)
    {
        if (visy[y])
            continue;
        double tmp = lx[x] + ly[y] - G[x][y];
        if (eq(lx[x] + ly[y], G[x][y]))
        {
            visy[y] = true;
            if (linker[y] == -1 || dfs(linker[y]))
            {
                linker[y] = x; // 匹配
                return true;
            }
        }
        else if (slack[y] > tmp)
            slack[y] = tmp;
    }
    return false;
}

void KM() // 二分图最大权值匹配
{
    memset(linker, -1, sizeof(linker));
    for (int i = 0; i < nx; ++i)
    {
        lx[i] = -inf;
        for (int j = 0; j < ny; ++j)
        {
            ly[j] = 0;
            if (G[i][j] > lx[i])
                lx[i] = G[i][j];
        }
    }
    for (int x = 0; x < nx; ++x)
    {
        for (int i = 0; i < ny; ++i)
            slack[i] = inf;
        while (true)
        {
            memset(visx, 0, sizeof(visx));
            memset(visy, 0, sizeof(visy));
            if (dfs(x))
                break;
            double d = inf;
            for (int i = 0; i < ny; ++i)
            {
                if (!visy[i] && d > slack[i])
                    d = slack[i];
            }
            for (int i = 0; i < nx; ++i)
            {
                if (visx[i])
                    lx[i] -= d;
            }
            for (int i = 0; i < ny; ++i)
            {
                if (visy[i])
                    ly[i] += d;
                else
                    slack[i] -= d;
            }
        }
    }
}

double distance(int x1, int y1, int x2, int y2)
{
    return sqrt(1.0 * (x1 - x2) * (x1 - x2) + 1.0 * (y1 - y2) * (y1 - y2));
}

struct Node
{
    int x, y;
}nodea[maxn], nodeb[maxn];

int main()
{
    int cnt = 0;
    while (scanf("%d", &n) != EOF)
    {
        if (cnt++ > 0)
            printf("\n");
        nx = ny = n;
        for (int i = 0; i < n; ++i)
            scanf("%d%d", &nodea[i].x, &nodea[i].y);
        for (int i = 0; i < n; ++i)
            scanf("%d%d", &nodeb[i].x, &nodeb[i].y);
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j)
                G[j][i] = -distance(nodea[i].x, nodea[i].y, nodeb[j].x, nodeb[j].y);
        KM(); // 权值取相反数，问的是i的匹配，所以用的是G[j][i]，也可以单独记录
        for (int i = 0; i < n; ++i)
            printf("%d\n", linker[i] + 1);
    }
    return 0;
}

注意，必须得用两点间的欧几里得距离来求，因为是实际长度并非相对长度，我之前写的是return 1ll * (x1 - x2) * (x1 - x2) + 1ll * (y1 - y2) * (y1 - y2);WA到死。

在这里分享一组数据。

In.txt

out.txt

再分享一个刘汝佳老师的标程。

// LA4043 Ants
// Rujia Liu
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
 
const int maxn = 100 + 10;
const double INF = 1e30;
 
int n;
double W[maxn][maxn];
double Lx[maxn], Ly[maxn];   // 顶标
int left[maxn];          // left[i]为右边第i个点的匹配点编号
bool S[maxn], T[maxn];   // S[i]和T[i]为左/右第i个点是否已标记
 
bool eq(double a, double b) {
  return fabs(a-b) < 1e-9;
}
 
bool match(int i){
  S[i] = true;
  for(int j = 1; j <= n; j++) if (eq(Lx[i]+Ly[j], W[i][j]) && !T[j]){
    T[j] = true;
    if (!left[j] || match(left[j])){
      left[j] = i;
      return true;
    }
  }
  return false;
}
 
void update(){
  double a = INF;
  for(int i = 1; i <= n; i++) if(S[i])
    for(int j = 1; j <= n; j++) if(!T[j])
      a = min(a, Lx[i]+Ly[j] - W[i][j]);
  for(int i = 1; i <= n; i++) {
    if(S[i]) Lx[i] -= a;
    if(T[i]) Ly[i] += a;
  }
}
 
void KM() {
  for(int i = 1; i <= n; i++) {
    left[i] = Lx[i] = Ly[i] = 0;
    for(int j = 1; j <= n; j++)
      Lx[i] = max(Lx[i], W[i][j]);
  }
  for(int i = 1; i <= n; i++) {
    for(;;) {
      for(int j = 1; j <= n; j++) S[j] = T[j] = 0;
      if(match(i)) break; else update();
    }
  }
}
 
int main(){
  int kase = 0;
  while(scanf("%d", &n) == 1) {
    if(++kase > 1) printf("\n");
 
    int x1[maxn], y1[maxn], x2[maxn], y2[maxn];
    for(int i = 1; i <= n; i++) scanf("%d%d", &x1[i], &y1[i]);
    for(int i = 1; i <= n; i++) scanf("%d%d", &x2[i], &y2[i]);
    for(int i = 1; i <= n; i++) // ant colony
      for(int j = 1; j <= n; j++) // apple tree
        W[j][i] = -sqrt((double)(x1[i]-x2[j])*(x1[i]-x2[j]) + (double)(y1[i]-y2[j])*(y1[i]-y2[j]));
    KM(); // 最大权匹配
    for(int i = 1; i <= n; i++) printf("%d\n", left[i]);
  }
  return 0;
}

The end.
2018-08-24 星期五